教材«deeplearning»的读书笔记.
- 对于Chapter 9, 除了做笔记外, 还对部分地方做了扩展(主要来自于博客[2]), 如: 在 卷积函数的几个变体 中补充了分组卷积, 混洗分组卷积, 逐点分组卷积, 但笔记的整体结构仍然和教材对应, 最后, 单独做了一节Chapter 9 supplementary materials来对Chapter 9的笔记做一个补充.
目录
- Chapter 9. Convolutional Networks
- Chapter 9 supplementary materials
- Chapter 10. Sequence Modeling: Recurrent and Recursive Nets
- Reference
Chapter 9. Convolutional Networks
首先, 描述什么是卷积, 然后解释在神经网络里使用卷积的动机; 接着介绍pooling, 这是几乎所有卷积网络都会用到的操作, 通常情况下, 卷积网络中的pooling与工程或数学中的卷积定义是不一致的, 进而详细介绍卷积与pooling的关系; 然后, 介绍卷积函数的几个变体以及怎样利用卷积来处理具有不同数据维度的数据; 最后, 介绍几个可以使卷积操作高效运行的几个算法. 另外, 本文没有介绍如何选择合适的卷积网络结构, 而是主要致力于介绍卷积网络所具备的能力.
1. 卷积是什么:
卷积: 对其中一个函数做mirror, 然后平移t后与另一个函数相乘后做积分. 在实际应用场景, 我们处理的往往是离散信号, 因此积分要换成求和, 此外, filter往往是带限信号, 通过这种方式可以利用finite个元素的和实现infinite summation.
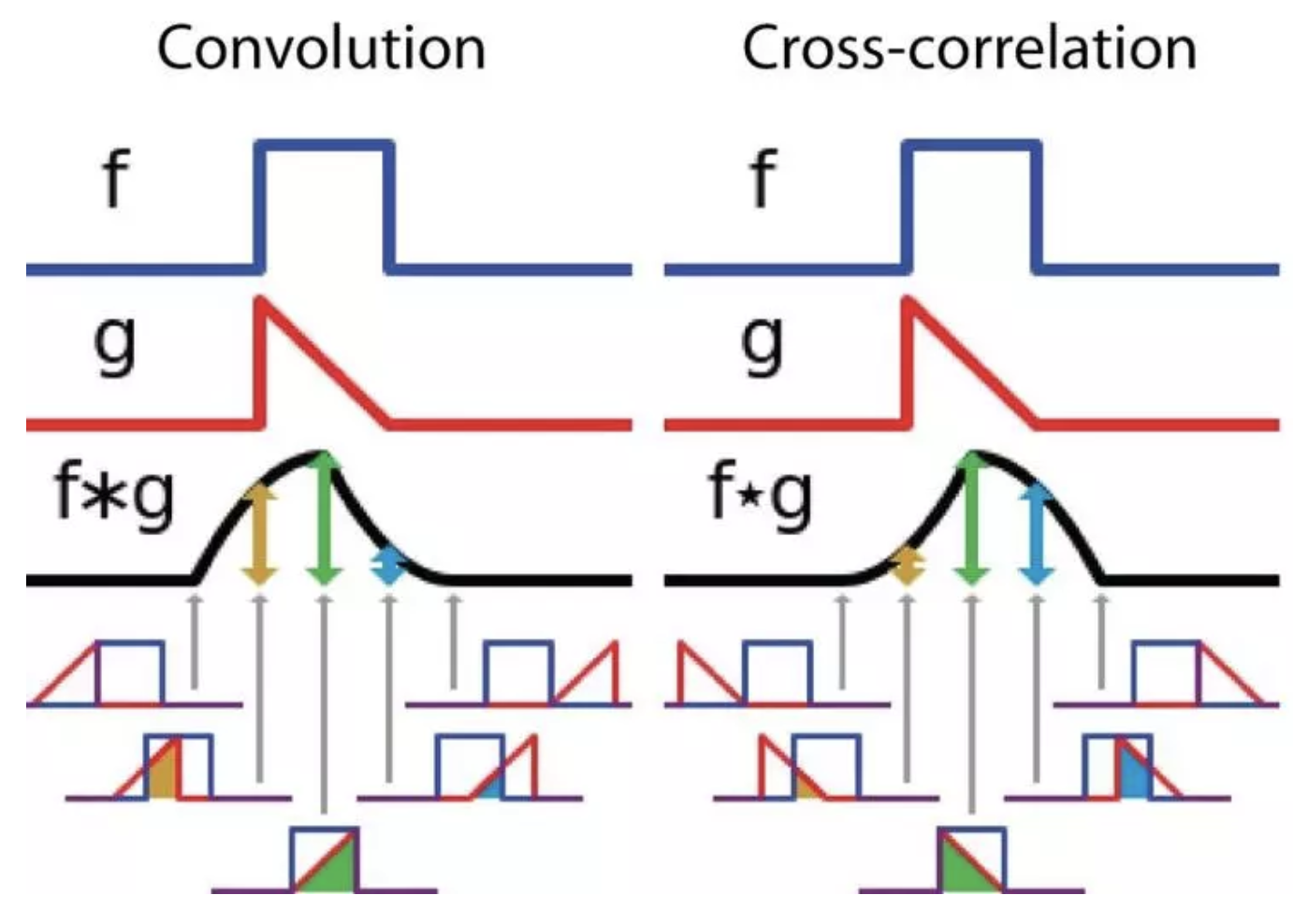
卷积定义中之所以要对其中一个函数翻转是为了使卷积具有 交换律. 这个性质可以通过画图来说明, 做法提醒: 分别翻转函数后又移, 与之做对比的做法为不翻转函数直接做右移. 另外, 与卷积相似的一个操作是互相关(cross-correlation), 该函数没有翻转而是直接右移(官方定义为左移第一个函数). 值得注意的是: 很多机器学习库将互相关叫做卷积. 在本文, 我们按照惯例也将卷积和互相关都称作卷积, 而在具体使用中明确声明是否对kernel进行翻转. 二者的区别如图所示:
离散卷积可以看成矩阵乘法, 只不过矩阵里的元素可以经变化而等于其他元素(shift). 以一维信号卷积为例, 由卷积核构成的矩阵的特点为: 上一行元素做一次shift后等于下一行元素(该矩阵叫做Toeplitz matrix).
2. 动机:
卷积通过三个重要的idea来改变机器学习系统: sparse interactions, parameter sharing, equivariant representations.
sparse interactions描述的是每个output unit和所有的input units之间的关系, 这个关系又叫做sparse connectivity or sparse weights. sparse interactions的好处是可以缩减模型的存储需求同时改善模型的统计有效性(statistic efficiency). 此外, sparse interactions也意味着 计算输出需要更少的操作. sparse connectivity与matrix-multiplication connectivity的区别: 1). 前者的每一个input unit会影响部分output units(稀疏度决定或者说kernel size决定), 后者的每一个input unit会影响所有的output units; 2). 前者的每一个output unit(ou)受部分iunput units(这部分units叫做ou的感受域–receptive field)的影响, 后者的output unit受到所有input units的影响; 3). 在卷积网络中深层的感受域要比浅层的感受域大, 这意味着, 在卷积网络中即使direct连接是sparse的, 但是深层次的in-direct却具有很大的覆盖范围.
在传统的神经网络中, 参数矩阵中的每一个参数都只用了一次; 在卷积网络中, 使用了parameter sharing, 也称作tied weights(即同一个weight paramter在使用时值是相同的). 对于描述同一个线性关系, 由于卷积的parameter sharing性质, 相较于传统的矩阵相乘会非常的节省空间以及减少计算量. 卷积的参数共享使层具有平移同变性的特点(equivariance to translation). 所谓的同变意味着: 输入改变, 输出以同样的方式改变. 具体来说, 如果满足$f(g(.)) = g(f(.))$, 那么函数$f(.)$对于另一个函数$g(.)$是同变的. 以卷积为例, 让$g(.)$代表对变量的shift, 那么卷积函数对于$g(.)$来说是同变的. 套用同变的定义的解释可以这样描述: 对input先做shift后做卷积, 等价于对input先做卷积再做shift. 参数共享的好处之一是可以检测同一模式(eg: 同样的边缘可能在一副图像上出现多次, 而parameter sharing可以保证这个边缘特征多次同变出现). 卷积对于尺度获旋转不具有同变性.
3. pooling:
卷积层主要包含三个阶段: 阶段一: 并行的执行几个卷积; 阶段二: 非线性化, 即每个output unit经过activation function, 这个阶段也叫做detector stage; 阶段三: 使用pooling函数修改输出, 如: max pooling. pooling的作用是: 对于小的input变化具有不变性(invariant), 换句话说, 对input做一个小的平移, pooling后的结果保持不变. 如果我们关心的是某些特征是否存在而不是它的确切位置, 那么不变性这个性质就尤为重要. 从另一个角度来看, 不变性在一定程度上可以维持特征的位置.
使用pooling相当于使用了这样的先验知识: 如果layer学到的function对于small translation具有不变性. 假如这个假设成立, 那么pooling可以改善网络的统计有效性(statistic efficiency). 除了直接在空间域使用pooling, 还可以在多通道之间使用pooling, 从而学习对输入的其他变换的不变性(如: 旋转不变性). 另外, pooling的好处还可以减小计算量.
pooling对解决许多任务中的尺寸各异的input问题都是必要的, 以分类尺寸各异的图片为例: 在分类层, 我们一定要提供一个固定尺寸的input以供分类, 这通常要通过动态pooling的方式做到(调节pooling region之间的offset). 这就涉及到了如下几个话题:
- 在不同的情形如何选择不同的pooling(Boureau et al., 2010)
- 如何动态的pool feature together, eg: 将聚类算法应用在感兴趣的特征(Boureau et al., 2011), 学习一个单一的pool 结构, 然后应用到所有图像上(Jia et al., 2012)
pooling可以使一些利用了top-down信息的神经网络结构(如: Boltzmann machines或autoencoders)变得复杂, 这些话题会在 part III中讨论, 在20.6中讨论如何poolingconvolutional Boltzmann machines; 20.10.6讨论了一些可微网络所需要的逆pooling操作(在pooling unit上执行inverse-like operation). 图9.11讨论了几个使用了卷积和pooling的卷积网络结构.
4. 卷积和pooling:
首先介绍prior的强弱, 这里提到的程度指的是对参数的决策, 越强就代表越可能对参数做出决策, 例如, 具有较大variance的高斯分布(entropy大)就是弱prior, 反之就是强prior; 进一步, infinitly prior就是将一部分参数的概率置0, 也就是直接决策. 而卷积和pooling都是强prior, 卷积网络等价于基于强prior的全连接网络, 这里的强prior有两层含义: 1). 参数共享 2). 局部交互性; 类似地, pooling的强prior为: feature对small translation具有不变性.
当然, 以强prior的全连接网络来实现卷积网络肯定是不划算的, 但是以这种方式来思考卷积网络可以帮助我们洞察其是如何工作的: underfitting, 简而言之, 当强prior的假设不成立的时候就会引起underfitting.
5. 卷积函数的几个变体:
在神经网络里提到的卷积在应用层面上是有别于数学上的卷积的, 这主要体现在以下几个方面:
1. 神经网络的卷积指的是多个可并行执行的卷积, 即多通道卷积, 因为一个kernel只能捕捉到一个模式的特征, 而我们通常想要神经网络的每一层可以捕捉到多模式的特征.
2. 由于神经网络中的卷积通常是多通道卷积, 因此该卷积即使带flipping也不具有交换性(画画图就可以知道); 此外, 在实际应用中input tensor V中的元素为$V_{l, j, k}$, kernel tensor K中的元素为$K_{i, l, m ,n}$, output tensor Z中的元素为$Z_{i, j, k}$, 其中, input tensor和output tensor的index索引意义相同, 即: channel 索引, row 索引, column 索引, kernel tensor的索引意义为: kernel 索引, channel 索引, row 索引, column 索引, 此外, kernel tensor的索引意义还可以表示为: output元素的channel索引, input元素的channel索引, 行偏移量, 列偏移量, 由此可得小技巧: 先$Z_{i, j, k}$, $V_{l, j, k}$, 然后再确定$K_{i, l, m ,n}$. 所以可得:
\[Z_{i, j, k} = \sum_{l, m, n} V_{l, j+m-1, k+n-1} K_{i, l, m, n} \tag{1}\]如果考虑到$s$ stride的情形(即每个维度都每s个值来一发, 换个说法就是每滑动一次就移动了$s$ 个像素), 则有
\[Z_{i, j, k} = \sum_{l, m, n} V_{l, (j-1)\times s+m, (k-1)\times s+n} K_{i, l, m, n} \tag{2}\]在实做的时候, 通常要对input做zero padding, 这样我们可以独立调节kernel size和output size. 这里讨论zero-padding的三个特殊情形: case 1, 不使用zero-padding, 并且只有包含整个kernel菜执行卷积运算(MATLAB称之为valid convolution), 这种设置的特点是output的每个pixel都来自于同样数量的input pixel, 如果input的宽度为m, kernel的宽度为l, 那么输出的宽度为m-l+1, 因此kernel越大, 衰减越严重, 随着layer的增多, output的维度最终会衰减至1; case 2, zero-padding使output的大小finput的大小相同, 0的个数为kernel size-1(两头补), (MATLAB称之为same convolution); case 3, 两头zero-padding, 补2k-2个0后, input为m+2k-2, output为m+k-1(MATLAB称之为full convolution). 通常在实做的时候, zero-padding的个数介于valid和same之间.
有时候, 我们只想利用局部连接性, 而不要parameter sharing, 这叫做locally connected layers, 又叫做unshared convolution, 其实, 这跟卷积也差不多, 关键区别在于不再共享kernel, 这也就意味着W(kernel)会多出两个维度j, k用以区分各个像素的kernel, 即:i 为output的channel索引, j为行索引, k为列索引, l为输出channel的索引, m为行偏移量, n为列偏移量, 输出与输入的关系变为:
\[Z_{i, j, k} = \sum_{l, m, n} V_{l, j+m-1, k+n-1} W_{i, j, k, l, m, n} \tag{3}\]注意, W与K差不多, 只不过多了j, k两维用以区分input各个pixel的weight(也就是说pixel之间不再sharing parameter了). locally connected layers适用于: 我们仅假设特征由局部input space决定, 而不能假设特征是位置无关的, eg: 如果我们想要知道一张image是否是人脸image, 我们仅需要在图像的下半部分寻找嘴巴.
此外, 为了进一步的缩减参数, 还可以减少每个kernel的规模, 这意味着仅利用input的几个channel而不是原来的所有channel, 一种标准实现就是: 将input的channel和kernels分同样的组, 然后组内采用卷积或者locally connected layers. 对于组内采用卷积的这种操作又叫做 分组卷积.
接下来插入一些分组卷积的补充材料: 分组卷积, 混洗分组卷积和逐点分组卷积, 当然, 可以将这部分扩展跳过去阅读.
2012年的AlexNet[9]对分组卷积进行了介绍, 分组卷积在上面的教材笔记上已经介绍了, 这里做个总结: 在分组卷积中, 过滤器被拆分为不同的组, 每一个组都负责具有一定深度的传统2D卷积的工作. 分组卷积的优势为:
- 训练高效: 由于卷积被拆分到几条路线中, 每条路线都由不同的GPU分别进行处理. 这一过程就允许模型以平行的方式在多个GPU 上进行训练. 对于训练非常深度的神经网络,分组卷积变得很重要.
- 模型高效: 当过滤器组数增加时, 模型参数就会减少; 在标准的2D卷积中, 过滤器有$h \times w \times Din \times Dout$ 个参数, 而在拆分为2个过滤器组的分组卷积中, 过滤器仅有$h \times w \times Din/2 \times Dout/2 \times 2$ 个参数, 参数数量减少了一半.
- 分组卷积能提供比标准 2D 卷积更好的模型: 过滤器组似乎将学习的过滤器拆分成了两个不同的组: 黑白滤镜和彩色滤镜(有一篇不错的博客[10]详细阐述了这一点)
混洗分组卷积(Shuffled grouped convolution, 旷世提出的[11])背后的思路与分组卷积(应用于MobileNet、ResNet等网络)以及深度可分离卷积(应用于Xception)背后的思路相关, 总的来说, 混洗分组卷积包括分组卷积和通道混洗(channel shuffling)[2], 所谓的通道混洗就是通道混洗的思路就是混合来自不同过滤器组的信息, 如图所示:.
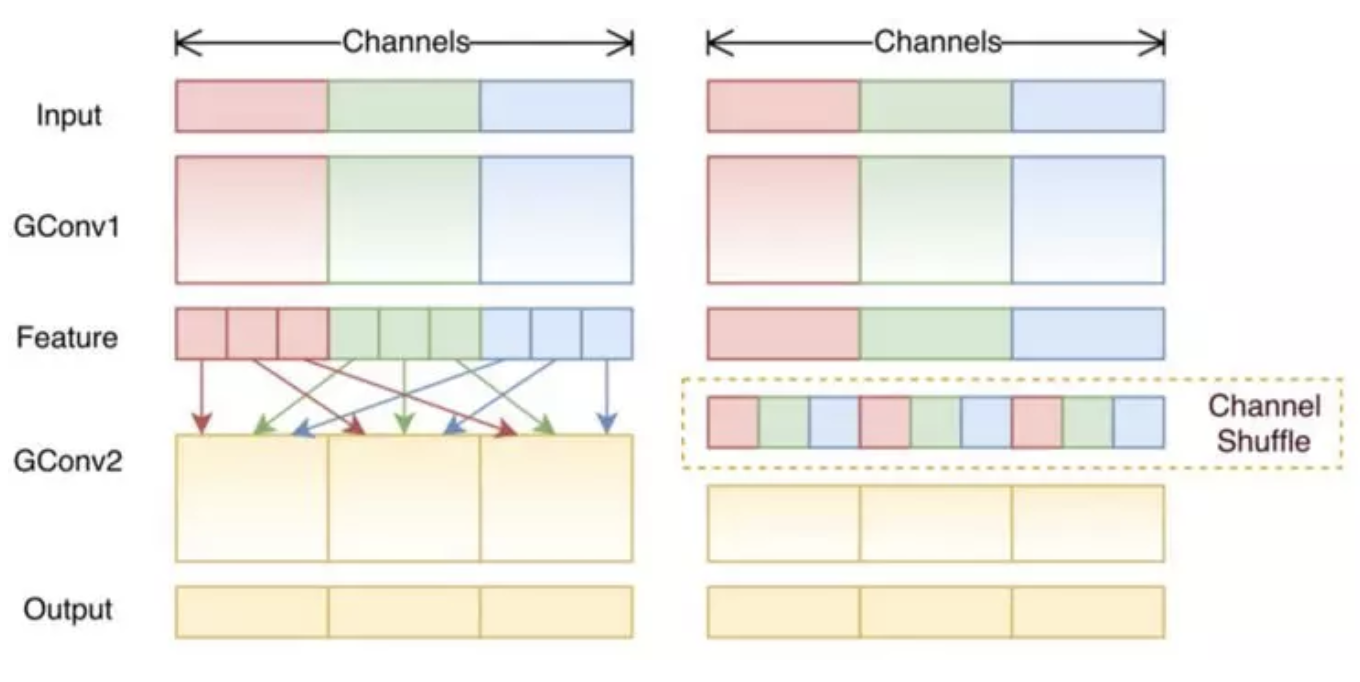
在应用有3个过滤器组的第一个分组卷积GConv1后得到了feature map, 然后, 先将每个组中的通道拆分为几个小组, 再混合这些小组. 经过通道混洗, 我们再接着如常执行第二个分组卷积GConv.
逐点分组卷积(Pointwise grouped convolution)是针对1x1卷积进行分组操作, 该操作与分组卷积的相同[11].
旷世的ShuffleNet[11]使用了: 1. 混洗分组卷积; 2. 逐点分组卷积; 3. 深度可分离卷积. 该架构设计能明显地减少计算量同时还能保持准确性, 在实际的移动设备上, ShuffleNet的分类错误与AlexNet的相当. 然而, 从使用AlexNet的720 MFLOPs到使用ShuffleNet的40–140 MFLOPs, 计算成本明显下降. 在面向移动设备的卷积神经网络领域, ShuffleNe 以相对较小的计算成本以及良好的模型性能广受欢迎.[2]
在locally connected layer和convolutional layer之间我们可以很自然的想到一种中间模式, 即: 将input划分成一定规模的region, 然后region里执行locally connection, 而各个region进行parameter sharing, 这种方式称作tiled convolution(region内权重各异, region间共享参数). 图9.16对比了locally connected layers, tiled convolution, and standard convolution.
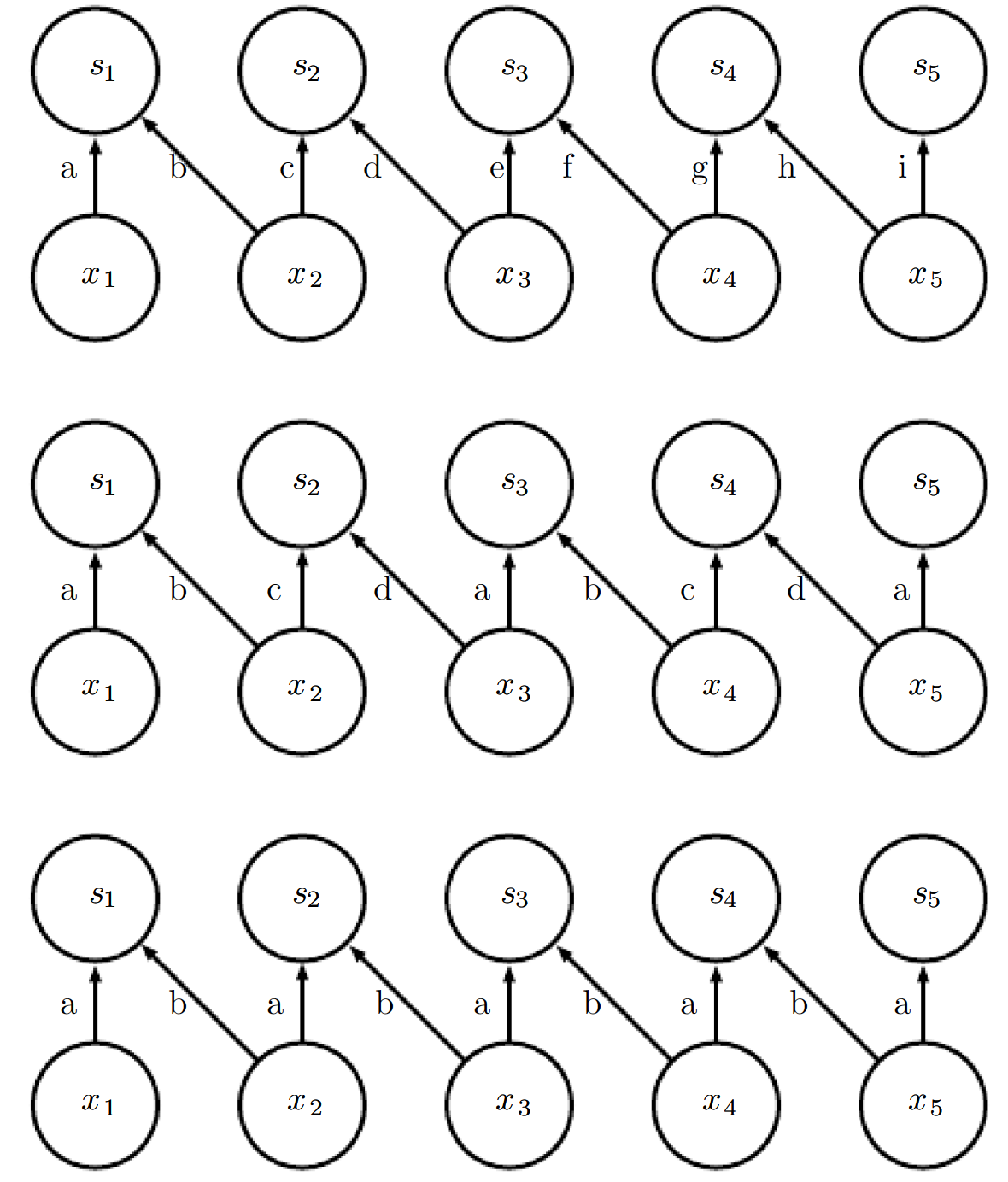
tiled convolution的kernel与标准卷积的kernel还是差不多, 只要加两个索引用以索引region里各个像素的独有weight就可以了m, 这里的输出输入关系就不写了(记得补一张三种形态下的kernel图).
由于tiled convolution的region内的filter以及localy connected layers内的filter是各异的, 因此这俩玩意儿经过max pooling后会有些有趣的现象: 假如各个filter学到了相同feature的不同transformed版本, 那么max-pooled后 units对这些学到的transformation具有不变性, 而标准的卷积很难做到这一点, 因为参数是共享的.
对于卷积网络的训练, Goodfellow (2010)详细推导了train过程中所需要的output对weight的梯度, output对input的梯度(用于backpropagation).
6. 利用卷积来处理具有不同数据维度的数据:
- structured outputs
经常讨论的一个议题是: 输出plane的size比输入plane的size要小, eg: 在单目标分类问题中, 空间维度的巨大缩减来自于大stride的pooling. 为了使输出的size与输入的相似, 可以避免使用pooling(Jain et al., 2007); 另外一个策略是输出一个更低分辨率的网格标签(Pinheiro and Collobert, 2014, 2015); 最后, 理论上可以使用单位stride的pooling.
举个图像语义分割的例子, 一种策略为: 首先产生像素-label的概率分布, 然后利用近邻像素(涉及到具体的建模)通过数次迭代来对这个概率分布进行refine, 在每一个步骤都会使用一些卷积操作, 这种策略叫做recurrent convolutional network, 如图:
语义分割之后, 有很多方法可以这个预测结果来对图像进行划分(Briggman et al., 2009; Turaga et al., 2010; Farabet et al., 2013), 通常情况下, 这些方法会基于这样一个假设: 相邻相似像素具有同样的标签. 图模型可以描述相邻像素的概率关系, 另外, 卷积网络可以极大化图模型的近似解(Ning et al., 2005; Thompson et al., 2014).
- data types
卷积网络使用的数据通常有几个channel, 详细的例子可以参考教材的表格9.1.
到此为止, 我们讨论的输入数据都是具有同样空间域维度的, 而卷积网络的一个优势就是可以处理不同空间域维度的数据, eg: 考虑一个尺寸各异的图像数据集, 直接建立一个固定尺寸的权值矩阵模型是不容易的, 而卷积却可以直接应用, 差别在于: kernel被利用的次数是由input的size决定的, 相应的卷积后的输出由这些计算次数决定. 有时候网络的输出可以是具有不同size的, 尤其对于语义分割问题, 不需要有额外的设计, 但是对于输出必须是固定尺寸的问题, 就需要有些额外的设计了, eg: 插入一个pooling layer使得pooling region同input的size是成比例的, 这样就可以使输出的尺寸固定. 使用卷积处理尺寸各异的数据是有条件的, 即: 数据具有同样的模式, 而区别在于模式的数值, 换句话说是对同样东西的不同观测; 如果数据的尺寸各异是由于模式的不同而引起的, 那么卷积就没有意义了.
7. 几个高效的卷积算法:
如果units个数众多, 比如超过一百万, 那么利用并行计算单元来加速卷积是必要的; 然而, 在许多情况下, 仅仅通过选择合适的卷积算法就可以达到加速的目的. 利用傅立叶变换性质, 先转到频域, 然后做点乘再反变换回来在某些问题里要比直接利用卷积快.
- 空间可分离卷积(spatially separable convolution)
这里讨论一下kernel是separable的情况, 教材是针对d-dimensional kernel进行阐述的, 为了便于理解, 举一个空间可分离卷积在2D图像上的应用: 假设卷积核为mxm的, 图像为NxN的, 在0填充情况下进行卷积, 常规做法需要的乘法运算次数为:
\[(N-m+1)(N-m+1)\times m \times m \tag{4}\], 而空间可分离卷积的运算次数为
\[(N-m+1)\times N \times m + (N-m+1)(N-m+1)\times m \tag{5}\], 空间可分离卷积与常规卷积的比例为:
\[\frac{1}{m} + \frac{1}{m(1-\frac{m-1}{N})} \tag{6}\]当$N\gg m$时, 比例就变成了$2/m$, 这就意味着在渐进意义下, 空间可分离卷积与常规卷积的运算次数的比例为$2/m$, 虽然空间可分离卷积可以减少计算成本, 但很少应用于深度学习, 一个主要原因是: 并不是所有的卷积核都是separable. 此外, 对于2D可分离卷积的证明可以看这篇博客Proof of Separable Convolution 2D.(本小结关键字: performing convolution or approximate convolution without harming the accuracy of the model ).
- 深度可分离卷积(depthwise separable convolution)
相对于前者, 深度可分离卷积的应用较为普遍, 比如MobileNet和Xception. 深度可分离卷积分为两步:1. 深度卷积, 也就是单通道卷积; 2. 扩大深度, 深度指的是output channels的个数, 此处用d, 那么扩大深度指的是做d次1x1卷积, 卷积核为1x1xnum_of_input_channels. 整个过程如图所示:
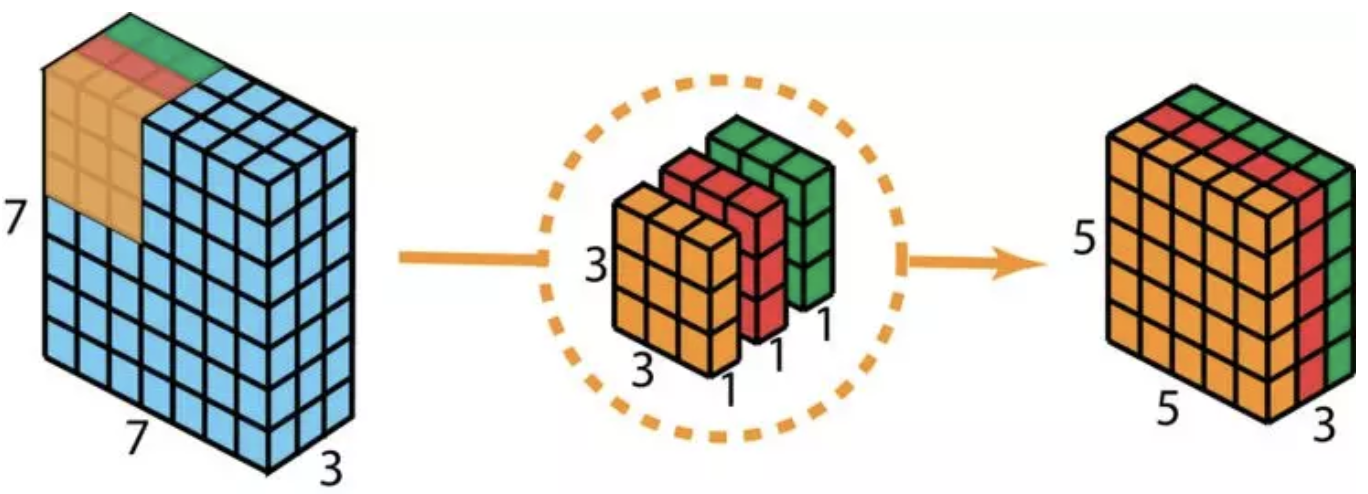
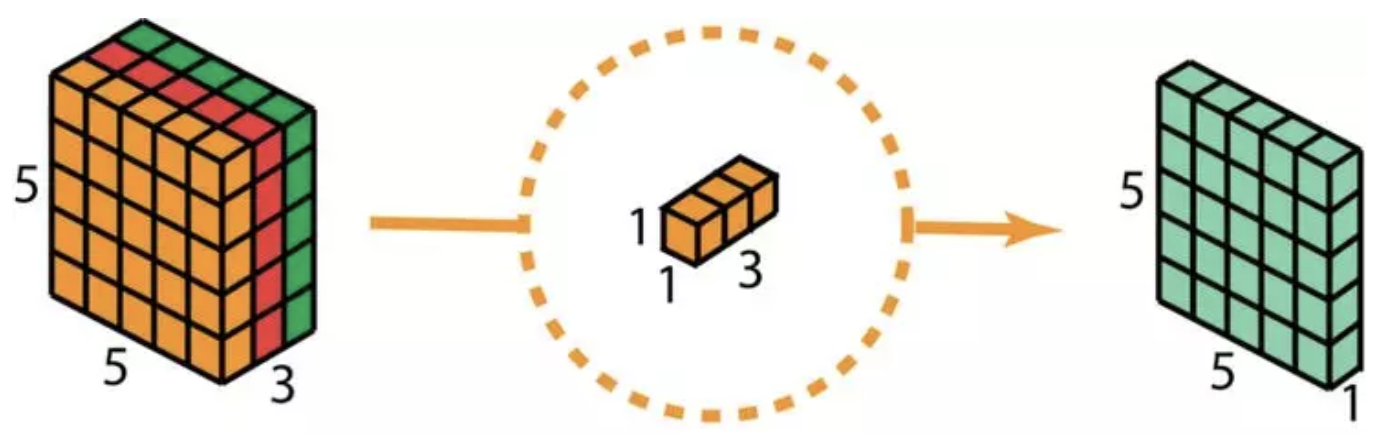
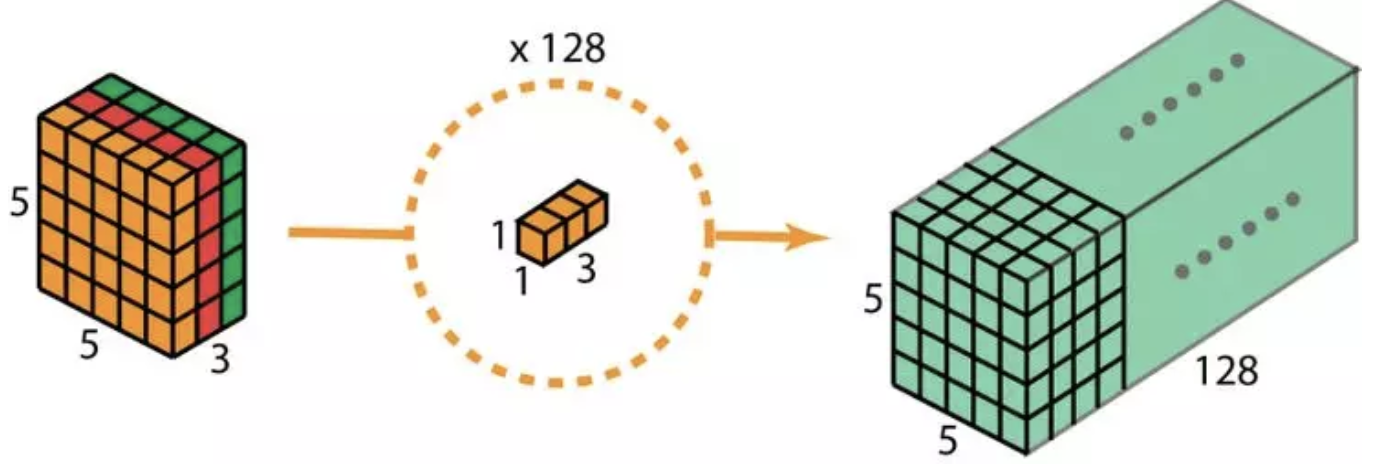
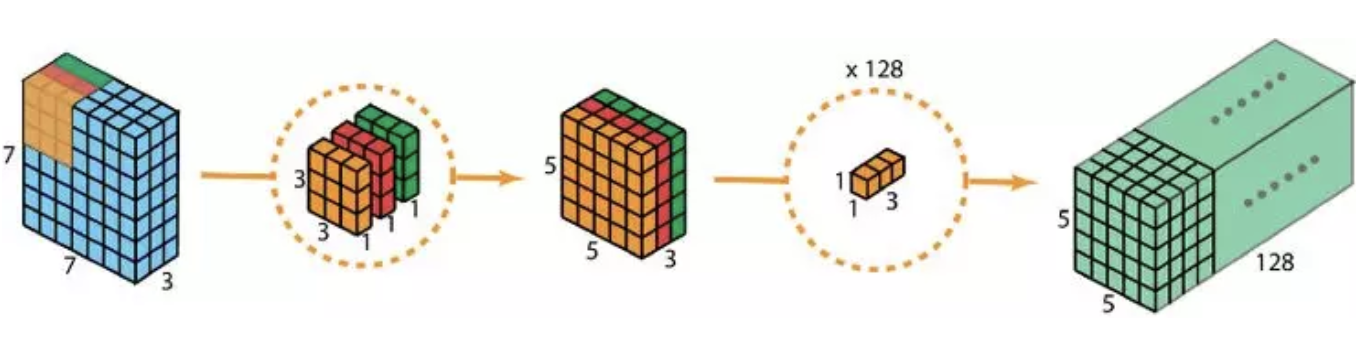
接下来对比下计算成本, 假如输入图像为$H\times W\times d$, 卷积核为$h\times h\times d$, 个数为$Nc$. 对于常规卷积, 所需要的乘法次数为:
\[(H-h+1)\times(W-h+1)\times h\times h\times d \times Nc \tag{7}\]而深度可分离卷积的乘法次数为:
\[(H-h+1)\times (W-h+1)\times d\times h\times h + (H-h+1)\times (W-h+1)\times d\times Nc \tag{8}\]公式8除以公式7得到比例:
\[\frac{1}{Nc} + \frac{1}{h^2} \tag{9}\]在实际应用中, Nc通常是成百上千的, 当$Nc \gg h$时, 上面的比例会变成$\frac{1}{h^2}$, 因此2D卷积的kernel为$3\times 3$时, 深度可分离卷积是常规卷积的$\frac{1}{9}$, 当kernel为$5\times 5$时, 这个比例为$\frac{1}{25}$. 由于深度可分离卷积会减少参数个数, 所以该方法可能会损害模型的性能, 尤其是小模型.
- random or unsupervised features
卷积网络训练主要应用于学习特征, 而输出层相对来说没那么大的计算开销, 这要是因为在经过几层的pooling之后, 提供给输出层的输入就是包含较少数量特征的向量. 在利用gradient descent执行监督训练时, 每一步梯度更新都要对整个网络运行一遍forward propagation和backward propagation. 因此一种减少开销的idea就是在训练过程中用一些不需要训练的特征.
有三种免训练策略来获得卷积核: 第一种: 随机初始化设定; 第二种: 人工设定, 比如通过设置来获得某一方向或者尺度上的边缘信息; 第三种: 通过无监督的方式来学习kernel, 比如Coates et al. (2011)利用k-means对小的image patches进行聚类, 然后把学习到的cluster中心当作卷积kernel. 在Part III中提到了很多无监督学习策略. 在训练前先用无监督方法学习到这些特征, 然后将这些特征在整个训练数据集上进行训练.
随机滤波(Random filter)在卷积网络中往往会惊人的好(Jarrett et al., 2009; Saxe et al., 2011; Pinto et al., 2011; Cox and Pinto, 2011). Saxe et al. (2011)表明: 在设定随机权重后, layers(卷积+pooling)会具有频率选择(frequency selective)不变性和平移不变性. 他们认为Random fiter提供了一种低开销的方式来选择卷积网络, 可以这样理解该说法: 如果是人工选择的话, 我们会只训练几个卷积网络的最后一层, 然后把表现最好的网络单拎出来, 然后再对该网络的网络结构进行整体的训练.
一种中间策略是, 仍然学习特征, 但是在参数更新的时候不需要对整个网络跑完forward和back propagation. 类似于多层感知机, 使用layer级别的贪婪策略来单独训练每一层, 也就是说单独训练第一层, 然后依据第一层训练得到的特征再训练第二层, 以此类推. Part III对第八章的supervised greedy layer-wise pretraining进行扩展, 探讨了用unsupervised 的方式来做greedy layer-wise pretraining. greedy layer-wise pretraing应用于卷积网络比较具有代表性的工作是Lee et al在2009提出的convolutional deep belief network. 卷积网络给了我们使用pretrain的机会, 比如: Coates et al在2011利用k-means对small image patch进行聚类, 然后利用这个patch-based model定义卷积网络的kernel, 这也就意味着可以利用unsupervised的方式来训练卷积网络, 利用这个策略会训练出非常大的模型同时使inference的时间增加(Ranzato et al., 2007b; Jarrett et al., 2009; Kavukcuoglu et al., 2010; Coates et al., 2013). 这个策略在2007~2013比较流行, 尤其在标签数据集比较少以及算力有限制的情况下. 如今, 通常采取纯粹的监督学习方式来训练整个卷积网络.
Chapter 9 supplementary materials
1. 3D卷积, 2. 1x1卷积, 3. 转置卷积(反卷积), 4. 空洞卷积, 5. 扁平化卷积
3D卷积就是3D卷积的一般化, 也就是filter的深度要小于input的深度, 运算的时候filter会沿着三个方向移动. 和对2D区域中目标的空间关系进行解码的2D卷积相似, 3D卷积也可以描述3D空间中目标的空间关系, 对于一些应用来说, 这种3D关系很重要, 例如在CT和MRI等生物医学图像的3D分割/重建中, 这些图像的目标如血管都是蜿蜒分布在3D空间中的[2].
计算方式如图:
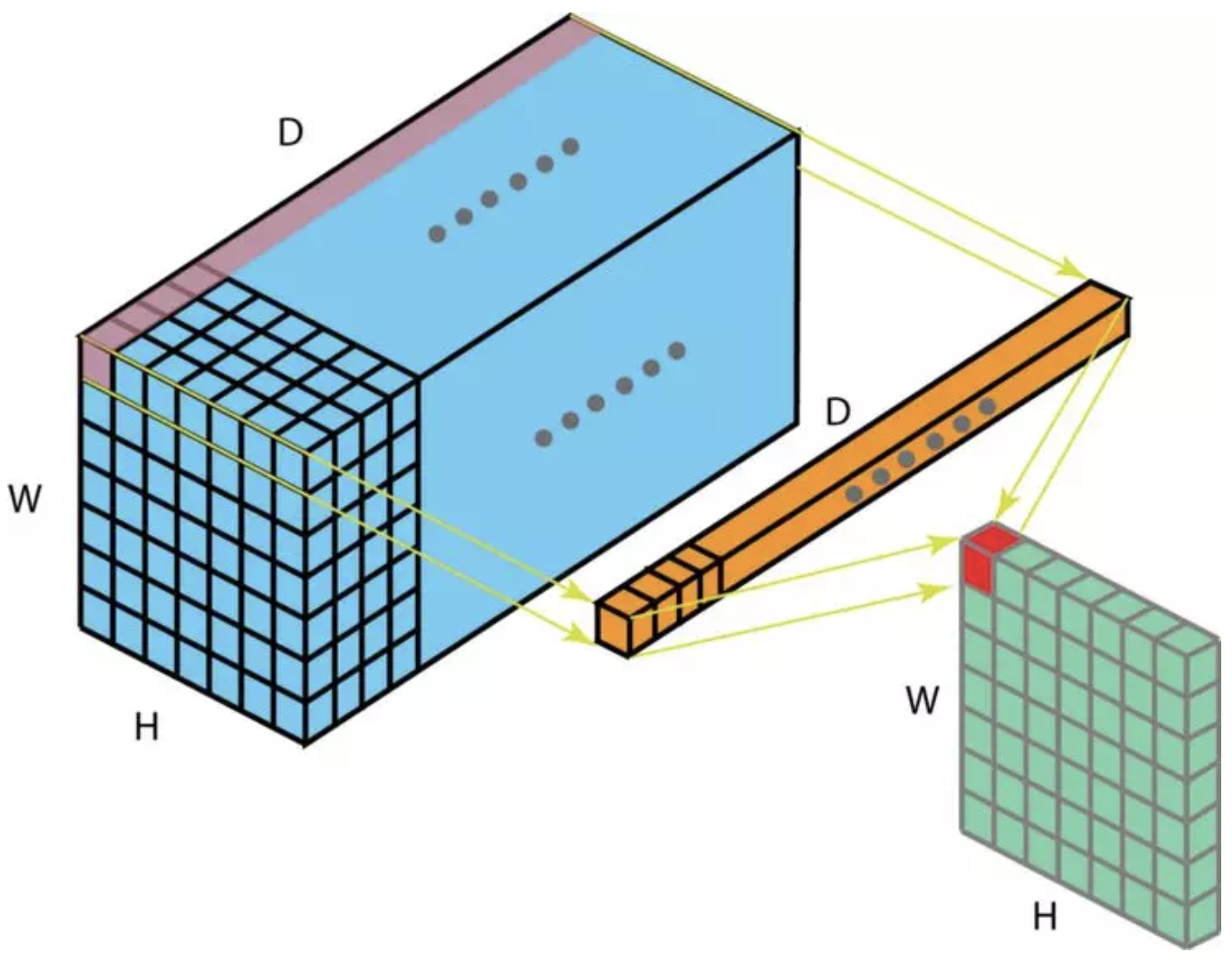
1x1卷积的好处有:
- 降维
- 对原特征进行有效的低纬嵌入
- 卷积以后反复应用非线性特征
扩展材料见1x1卷积.
从图像空间域尺度来看, 卷积可以执行下采样操作, 而转置卷积可以执行上采样操作. 对于上采样操作, 传统方法可以通过插值或手动创建规则来实现, 神经网络等现代架构则反过来趋向于让网络自己自动学习合适的转换, 而不需要人类的干预, 转置卷积便可以实现这一点. 转置卷积的应用场景有:1. 生成高分辨率图像;2. 自动编码器或语义分割中将低维特征映射到高维空间(语义分割首先在编码器中提取特征映射,然后在解码器中还原原始图像的大小从而能够在原始图像中对每一个像素进行分类). 转置卷积也叫做反卷积(deconvolution), 小数步长的卷积(fractionally strided convolution)[2].
转置卷积的计算方法为: 以input为2x2, 卷积核为3x3为例, 若生成4x4的输出, 需要
- 在input周围填充2x2的zero, 使输入尺寸为6x6
- 执行stride为1的卷积操作
通过上面两个步骤就可以实现一种转置卷积操作. 此外, 从矩阵乘法的角度来看, 卷积和转置卷积所对应的矩阵乘法中参数矩阵(卷积核构成的)从矩阵形态(并不是数值哦)来看是转置的关系, 这就是转置卷积中转置的由来, 当然也可以看出叫反卷积似乎不是很合理.
棋盘效应(checkerboard artifacts)是研究人员在使用转置卷积时可以观察到的现象, 如图所示. 造成棋盘效应的原因是: 转置卷积的不均匀重叠(uneven overlap)使图像的某个部位的颜色比其他位置的深[5], 对于详细分析可以看[5]. 在应用转置卷积时, 可以做两件事情来减轻这种效应: 第一, 确认使用的过滤器的大小是能够被卷积步长整除的, 从而来避免重叠问题; 第二, 可以采用卷积步长为1的转置卷积来减轻棋盘效应. 然而, 正如在最近许多模型中所看到的, 这种效益依旧可能会显露出来[2]. 这篇论文进一步提出了一个更好的上采样方法: 首先调整图像大小(使用最近邻域内插法(Nearest Neighbor interpolation)和双向性内插法(bilinear interpolation)), 然后制作一个卷积层, 通过这样做, 论文作者成功避免了这一棋盘效应.

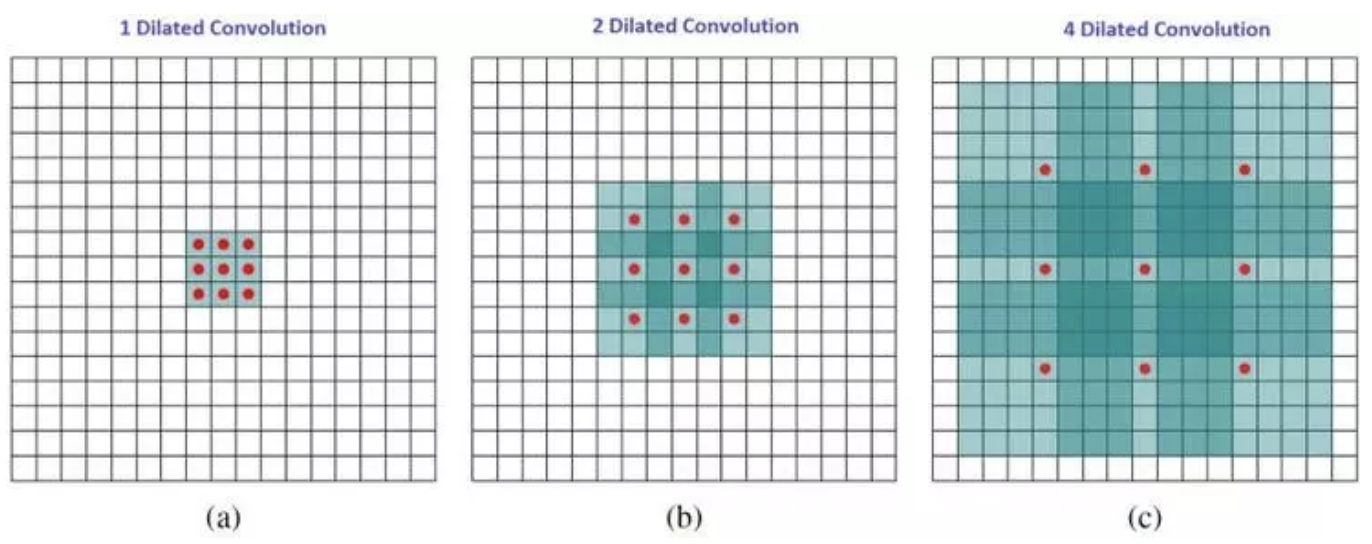
空洞卷积(Dilated Convolution)又叫做扩张卷积(Atrous Convolution), 所谓的空洞指的是input感受域不再是连续的, 而是有一定的间距, 当然, 间距为0的时候, 空洞卷积就会退化成标准的卷积, [2]关于这部分内容有一个比较好的动图, 可以看一下.
直观上, 空洞卷积通过在卷积核部分之间插入空间让卷积核膨胀, 这个增加的参数l(空洞率)表明了我们想要将卷积核放宽到多大. 虽然各实现是不同的, 但是在卷积核部分通常插入l-1空间. 下图显示了当l-1, 2 ,4 时的卷积核大小[2]. 在图像中, 3x3的红点表明经过卷积后的输出图像的像素是3x3. 虽然三次空洞卷积都得出了相同维度的输出图像, 但是模型观察到的感受野(receptive field)是大不相同的. l=1时, 感受野为3x3; l=2 时, 感受野是7x7; l=3 时, 感受野增至15x15. 有趣的是, 伴随这些操作的参数数量本质上是相同的, 不需要增加参数运算成本就能观察大的感受野. 正因为此, 空洞卷积常被用以低成本地增加输出单元上的感受野, 同时还不需要增加卷积核大小, 当多个空洞卷积一个接一个堆叠在一起时, 这种方式是非常有效的[2].
扁平化卷积(Flattened convolution)与空间可分离卷积类似, 即: 应用filter分离, 将标准的filter拆分为3个1D filters, 扁平化卷积与标准卷积的对比图如下:
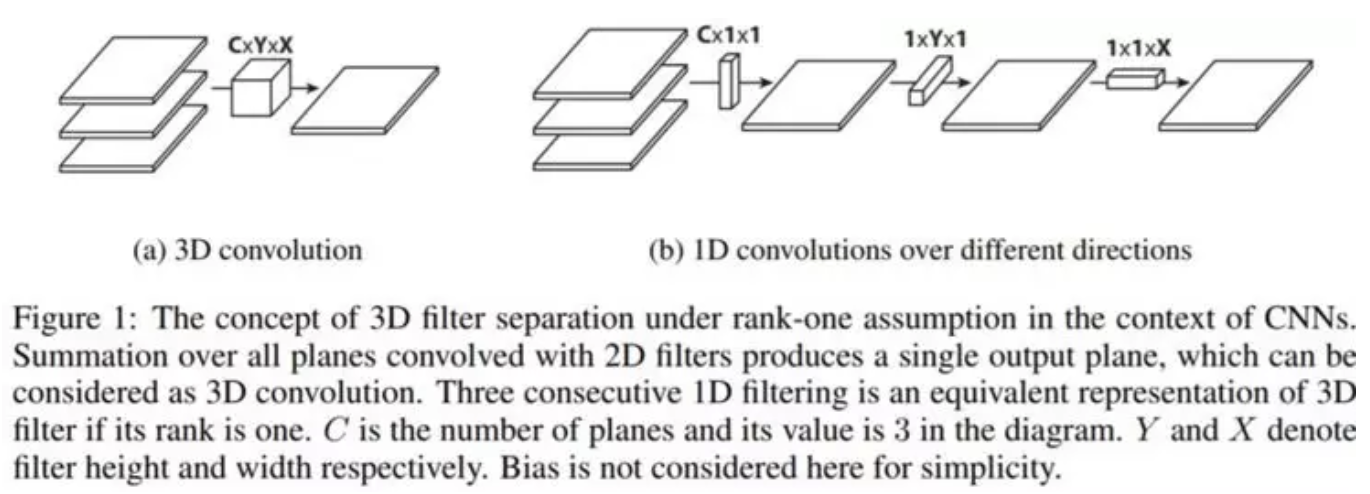
如果filter的rank是1, 那么便可以拆分成3个1D的filter的外积(注意扁平化卷积就是教材中提到的filter是separable, 只不过扁平化卷积指的是3D的情况). 但是在现实应用中, rank为1往往是不能被满足的. [8]指出随着分类问题的难度增加, 解决该问题还需要更多的关键部分. 深度网络中学习filter具有分布的特征值, 并且将分离直接用于过滤器会导致明显的信息丢失. 为了减轻这类问题, [8]限制了感受野的关系从而让模型可以根据训练学习1D分离的filter. 通过使用由连续的1Dfilter组成的扁平化网络在3D空间的所有方向上训练模型, 能够提供的性能与标准卷积网络相当, 不过由于学习参数的显著减少, 其计算成本要更低得多.
Chapter 10. Sequence Modeling: Recurrent and Recursive Nets
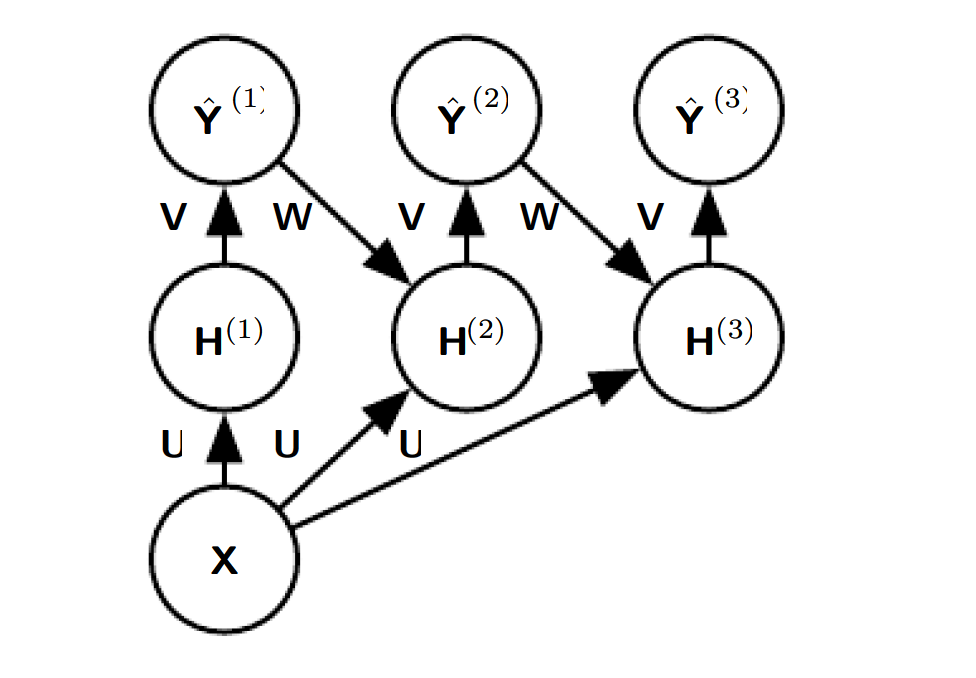
Recurrent and Recursive Nets(RNNs) 是一族专门处理序列数据的神经网络, 就像CNNs是专门处理图像数据一样, RNNs专门处理$x^1, x^2, .. x^\tau$这样的序列数据; 另外, 如CNNs可以很容易的处理大尺寸或者变尺寸图像一样, RNNs可以处理长序列或者变长序列数据.
10.2 Recurrent Neual Networks
首先, 10.1节介绍了两个基本的idea: 展开计算图、参数共享, 借助于这两个idea, 便可以设计大量的RNNs
Reference
Checkerboard artifacts
空洞卷积
Flattened convolutions
- 9. ImageNet Classification with Deep Convolutional Neural Networks
- 10. A Tutorial on Filter Groups (Grouped Convolution)
- 11. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
转载请注明:Mengranlin » 点击阅读原文
