目录
核磁共振成像
从本质上来讲, 核磁共振成像(MRI)是用硬件的方法实现傅立叶变换, 因此对人体扫描得到的是相应的频域数据(k-space data), 对采集得到的数据做逆傅立叶变换就得到了医生诊断所需的空间域图像, 流程如图所示:
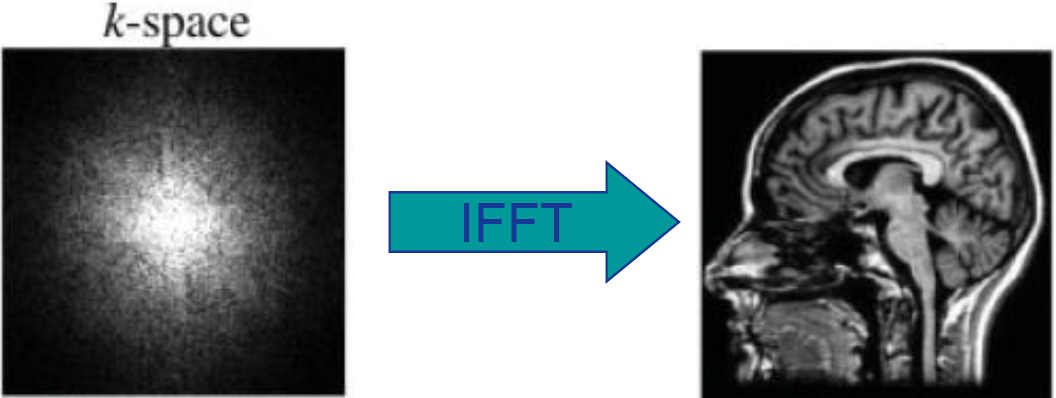
MRI的好处就不说了, 这里提一下其缺点, 进而引出这个研究方向的意义. MRI的主要缺点为:
- 扫描时间长(几分钟)
- 扫描过程中, 病人必须保持绝对静止
- 实时成像困难
当前的解决方案:
- 需要硬件支持的并行成像(我在MRI传统方法总结中介绍的SENSE就是这个场景下的一个成像方法)
- 减少采样数据
对于”减少采样量”, 如果不做任何处理, 根据Nyquist-Shannon采样定理, 重建图像会出现混叠现象. 如何在减少采样量的情况下, 尽可能的重建图像是MRI的研究内容之一, 同时这个问题刚好可以通过压缩感知(Compressed Sensing, CS)来描述.
压缩传感理论
相比于传统的数据压缩方式, 压缩传感最鲜明的特点是绕过了采样后再压缩这个比较低效的环节, 利用传感矩阵直接获得稀疏信号或者可压缩信号的特征信息, 如果对具有稀疏表示的原信号进行随机采样, 那么可以在突破奈奎斯特的条件下恢复出原信号. 为了更好的理解压缩传感, 本文首先介绍采样定理这一背景知识, 然后再引出压缩传感理论的模型以及实现.
采样定理
如果采样足够密集, 一个连续信号完全可以用其在等时间间隔点上的采样值来表示, 并且可以通过这些样本值把信号全部恢复出来, 这就是采样定理的内容. 采样定理的重要性在于:
- 在连续时间信号和离散时间信号之间起到桥梁作用, 换言之: 为离散信号表示连续信号提供了理论依据.
接下来建立采样, 首先用$x_p(t)=x(t)p(t)$表示一个带限(信号的傅立叶变换在某一有限频带范围外均为零)连续时间信号$x(t)$在均匀间隔上的采样. 如图2所示, 左图红色点代表$x_p(t)$, $\omega_{M}$代表$x(t)$的最高频率, 其中采样函数为$p(t) = \sum_{n=-\infty}^{\infty}\delta(t-nT)$, $T$为采样周期, $\omega_{s} = 2\pi/T$为采样频率.
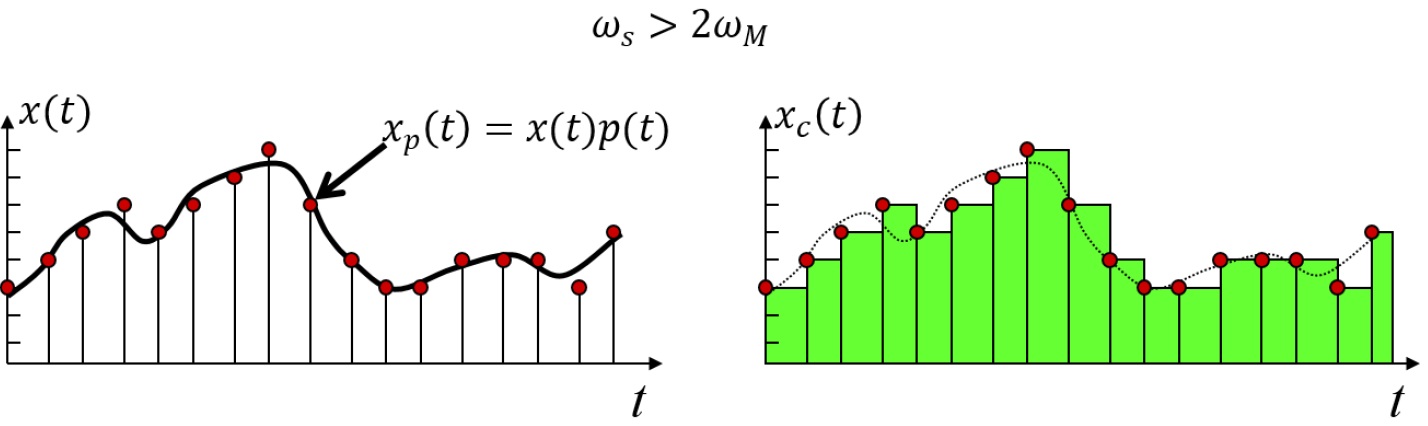
由傅立叶变换的相乘性质, 我们可得到:
\[X_p(j\omega) = \frac{1}{2\pi}[X(j\omega) * P(j\omega)] \tag{1}\]其中, $X(j\omega)$为原信号$x(t)$的频谱, $P(j\omega)$为$p(t)$的频谱, 表示为:
\[P(j\omega) = \frac{2\pi}{T} \sum_{k=-\infty}^{+\infty}\delta(\omega-k\omega_S) \tag{2}\]由$(1), (2)$可得采样频谱与原信号的频谱关系:
\[X_p(j\omega) = \frac{1}{T} \sum_{k=-\infty}^{+\infty}X(j(\omega-k\omega_{S}))) \tag{3}\]$(3)$表明$X_p(j\omega)$是$\omega$的周期函数, 由一组移位的$X(j\omega)$叠加组成, 但幅度为原信号频谱的$1/T$. 当$\omega_S > 2\omega_M$时, 互相移位的这些$X(j\omega)$并不发生重叠, 因此就能够用一个低通滤波器从$x_p(t)$中恢复出与原信号$x(t)$完全一致的重建信号$x_c(t)$(图2中右图虚线), 这一基本结果称之为采样定理. 采样定理要求采样频率必须大于$2\omega_M$, 而$2\omega_M$就称为奈奎斯特频率.
很明显, 有无限多个信号都可以产生一组同样的本值. 然而, 如果一个信号是带限的, 并且采样足够密集, 那么就可以从这一组本值中唯一的恢复出原信号, 这个结果就是采样定理.
压缩感知
相比传统的压缩方式, 压缩传感绕过了采样后再压缩这个比较低效的环节, 其利用传感矩阵直接获得稀疏信号或者可压缩信号的特征信息.
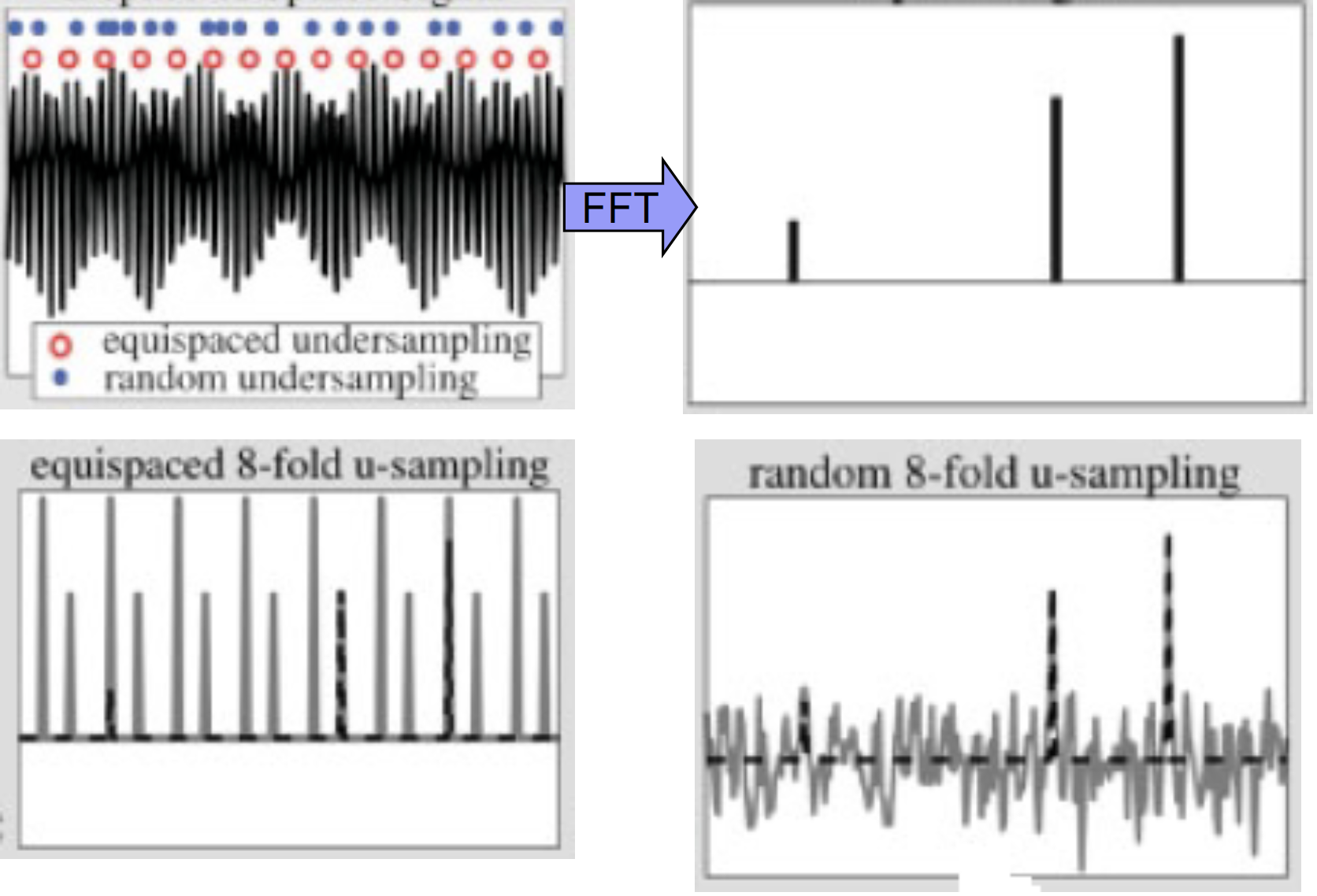
压缩传感表明: 如果对具有稀疏表示的原信号进行随机采样, 那么可以在突破奈奎斯特的条件下恢复出原信号. 为了描述压缩传感的这一特点, 我们通过图3的实验来进行说明. 如图3所示: 图中左上中的绿色点代表对原信号进行随机采样, 红色点代表对原信号进行等间隔采样. 右上是原信号的频谱, 左下是等间隔采样信号的频谱, 右下是随机采样信号的频谱. 通过对比三个频谱图发现等间隔采样下的频谱的混叠现象已经把原信号的频谱淹没, 而随机采样下的频谱的混叠结果更像是随机噪声. 因此, 通过对比两种采样模式下的频谱图, 发现在随机采样模式下可以更容易从采样信号恢复出原信号, 换句话说, 可以通过随机采样信号完美的恢复出原信号. 为了实现压缩传感,需要满足以下三个条件:
- 压缩传感要求采样是随机的.
- 压缩传感要求原信号具有稀疏表示(图3中的信号在恒等变换下具有稀疏表示), 信号越稀疏, 所需要的采样数据就越少.
- 压缩传感需要速度快且精度高的重建算法.
对于信号$x \in R^{Nx1}$, 我们可以通过它的$M$个线性测量, $s = \Phi x, \Phi \in R^{NxM}$. 其中, $\Phi$为传感器. 拥有了这$M$个随机测量和$\Phi$, 我们就可以在概率上完美的重构原始信号了. 实际上, 这看似神奇的现象是基于严格的数学优化问题. 下面以一维信号为例来引出压缩传感的数学模型.
对于一维信号$x$, 利用$MxN, M \ll N $ 的传感矩阵$\Phi$来拾取特征信息:
\[y = \Phi x \tag{4}\]设{$\psi_i$}$ _{i=1}^{N}$是由$N$x$1$列向量构成的正交基, $\Psi$为$N$x$N$的正交矩阵. 那么信号$x$具有稀疏度为k的稀疏表示, 表示为:
\[x \approx \sum_{i=1}^{K}\alpha_i\psi_i \tag{5}\]写成矩阵乘积的形式为:
\[x = \Psi \alpha \tag{6}\]将$(6)$带入$(4)$得:
\[y = \Phi \Psi \alpha \tag{7}\]压缩传感的传感过程如图4所示:
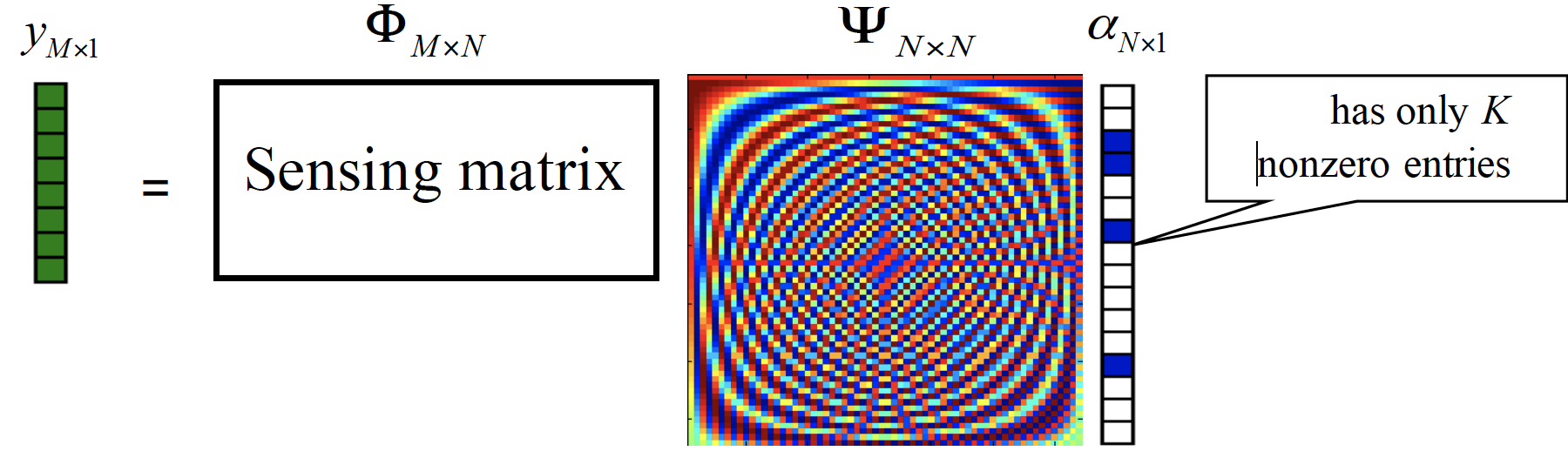
从图中我们可以认识到, 接下来的问题是: 在已知$y$和$\Phi$, 而且$x$在正交基$\Psi$中具有稀疏表示, 如何从$y$重建出$x$. 其中: 随机性要求$\Psi$与$\Phi$之间具有补相关性, 因此$\Phi$一般取高斯噪声矩阵.
公式7所描述的问题可以当成稀疏优化问题求解, 模型如下:
\[min \|\alpha\|_0 \quad s.t. \quad y = A\alpha \tag{8}\]其中, $A=\Psi\Phi$, 该问题是NP问题, 是计算不可解的, 因此用$l_1$范数代替, 模型如下:
\[min \|\alpha\|_1 \quad s.t. \quad y = A\alpha \tag{9}\]该问题是凸优化问题, 可以用线性规划方法进行求解.
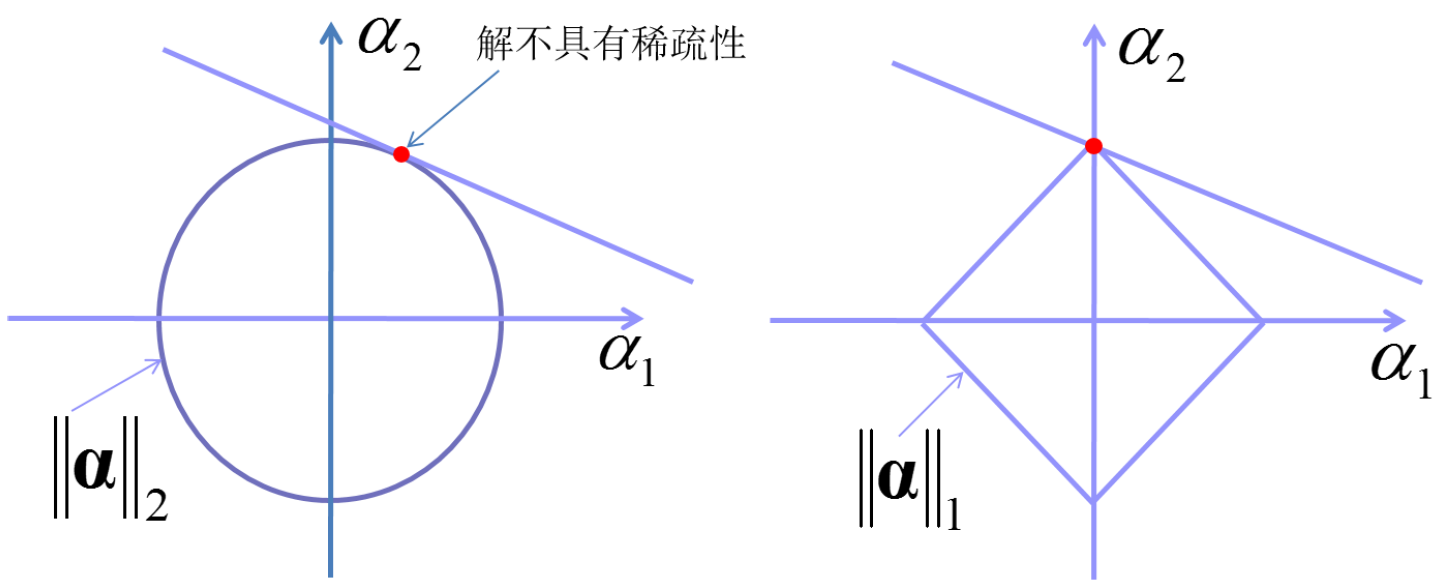
那么, 我们为什么选取$l_1$范数而不是$l_2$范数呢. 接下来我们通过图5进行说明: 以二维信号为例, 从图中我们发现$l_2$范数的单位圆与目标函数的交点通常在象限内,而不具有稀疏性,$l_1$范数的单位圆与目标函数的交点通常在坐标轴上, 从而具有稀疏性, 因此, 我们通常选取$l_1$范数作为我们的优化目标.
压缩感知在静态成像上的应用
如果不做任何处理, 根据采样定理, 重建出的图像会出现混叠现象. 那么在减少采量的情况下, 如何尽可能的重建图像是通过数学的办法来提高成像质量所面临的主要问题, 然而这正是压缩传感所解决的问题.
Lustig率先将压缩传感技术应用于核磁共振成像领域,其数学模型如下:
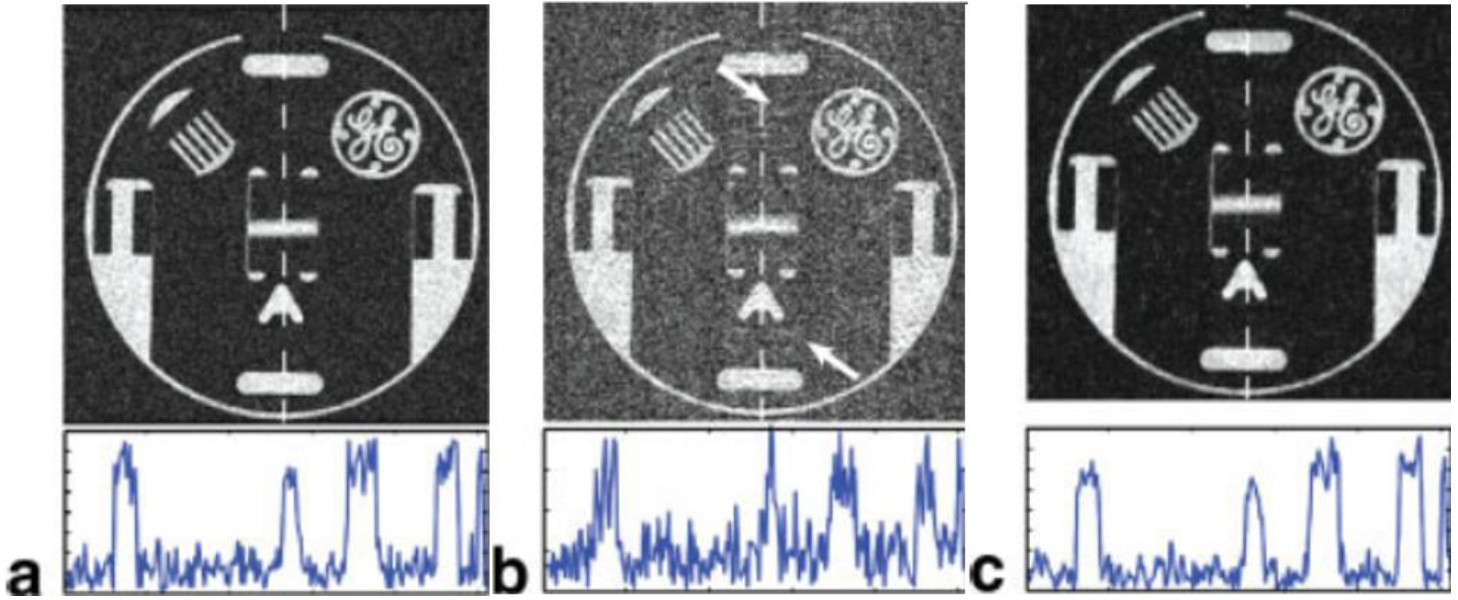
\[min \| \Psi m\|_0 \quad s.t. \quad \| \Phi_F m - y \|_2 < \varepsilon \tag{1}\]其中, $\Psi$代表稀疏变换, $\Phi_F m$代表部分傅立叶变换. 通过将该模型与前文所述的压缩传感模型对比发现, 压缩传感可以解决核磁共振成像问题. 在Lustig的实验中采用了小波变换作为稀疏矩阵, 实验结果如图所示:
我的工作
我的工作思路很简单, 主要从稀疏变换入手, 结合现有的主要的两类稀疏变换(预定义的、基于学习的)的优缺点, 提出了一个联合利用这两类变换来加强稀疏性的模型(GLSMRI):
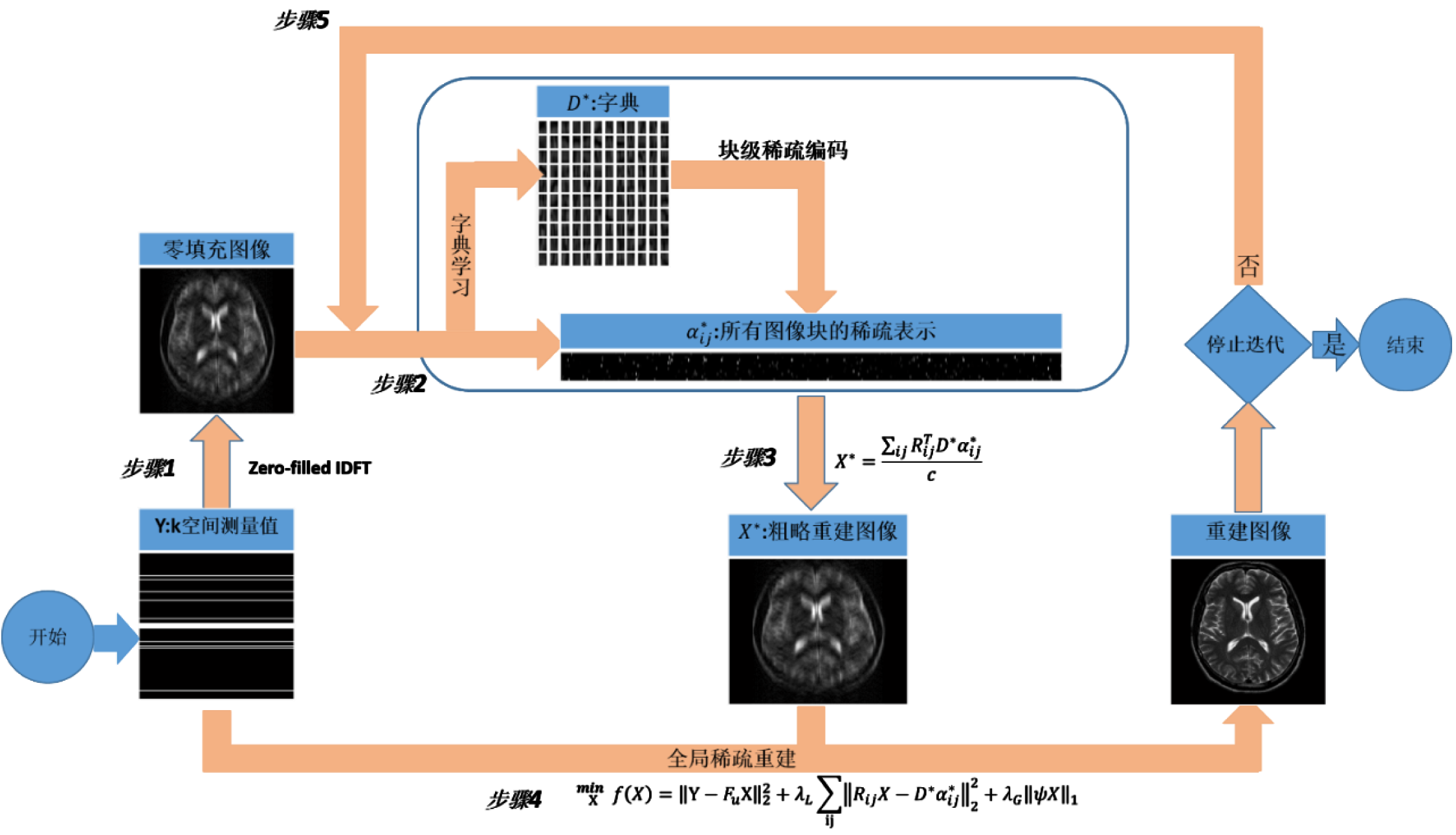
\[\min_{X, D, \Lambda } \{ \|Y - F_u X\|_2^2 + \lambda_L \sum_{ij} \| R_{ij} X -D \alpha_{ij}\|_2^2 + \lambda_G \| \Psi X \|_1 \} \tag{2}\]其中, 第一项为数据保真, 第二项为局部稀疏, 第三项为全局稀疏.
模型的求解比较常规, 即: 循环迭代如下两个步骤直至收敛:
- 对图像进行局部稀疏表示
- 在局部稀疏表示已知的条件下进行全局稀疏重建
算法流程如图所示:
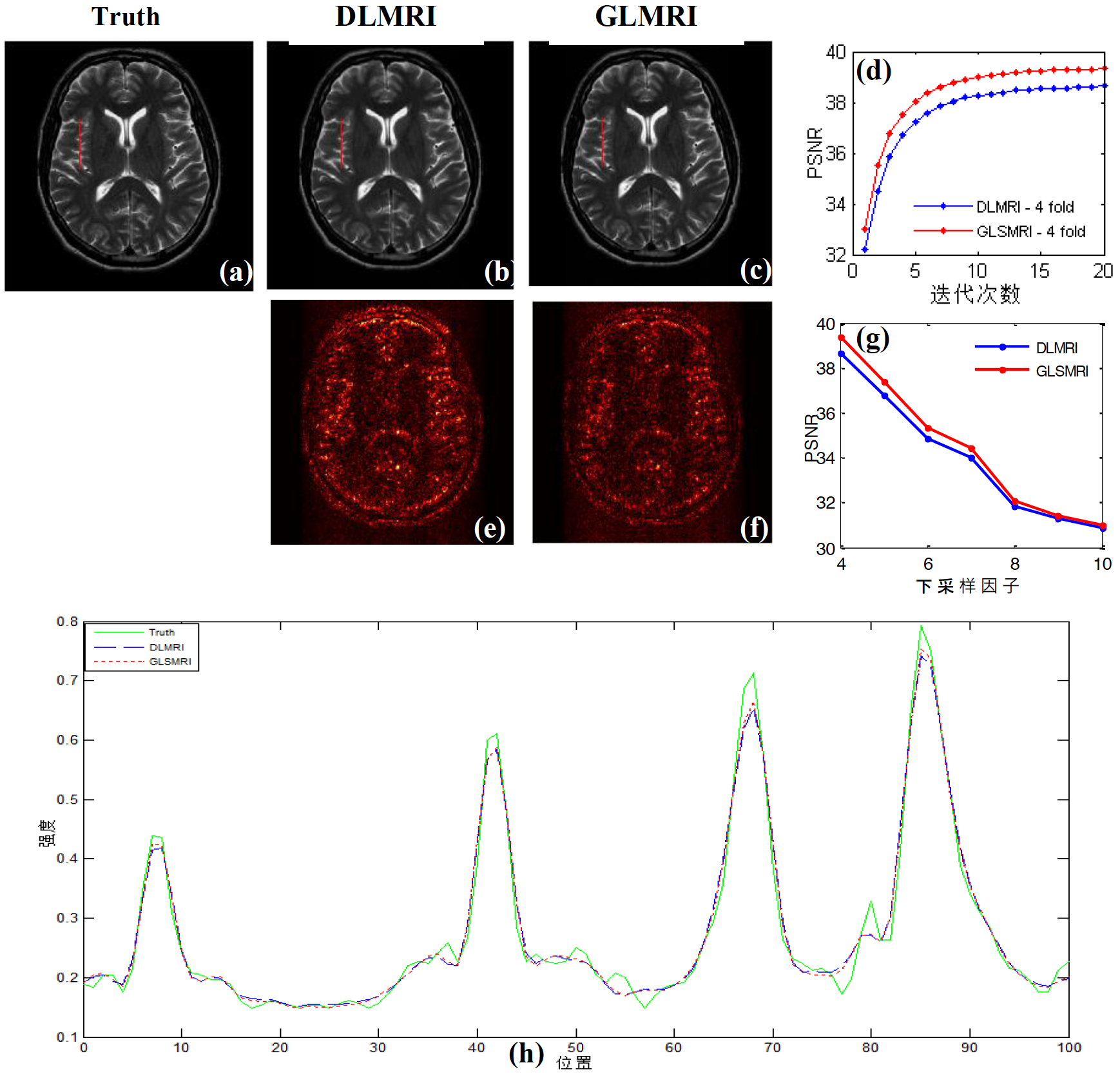
实验结果
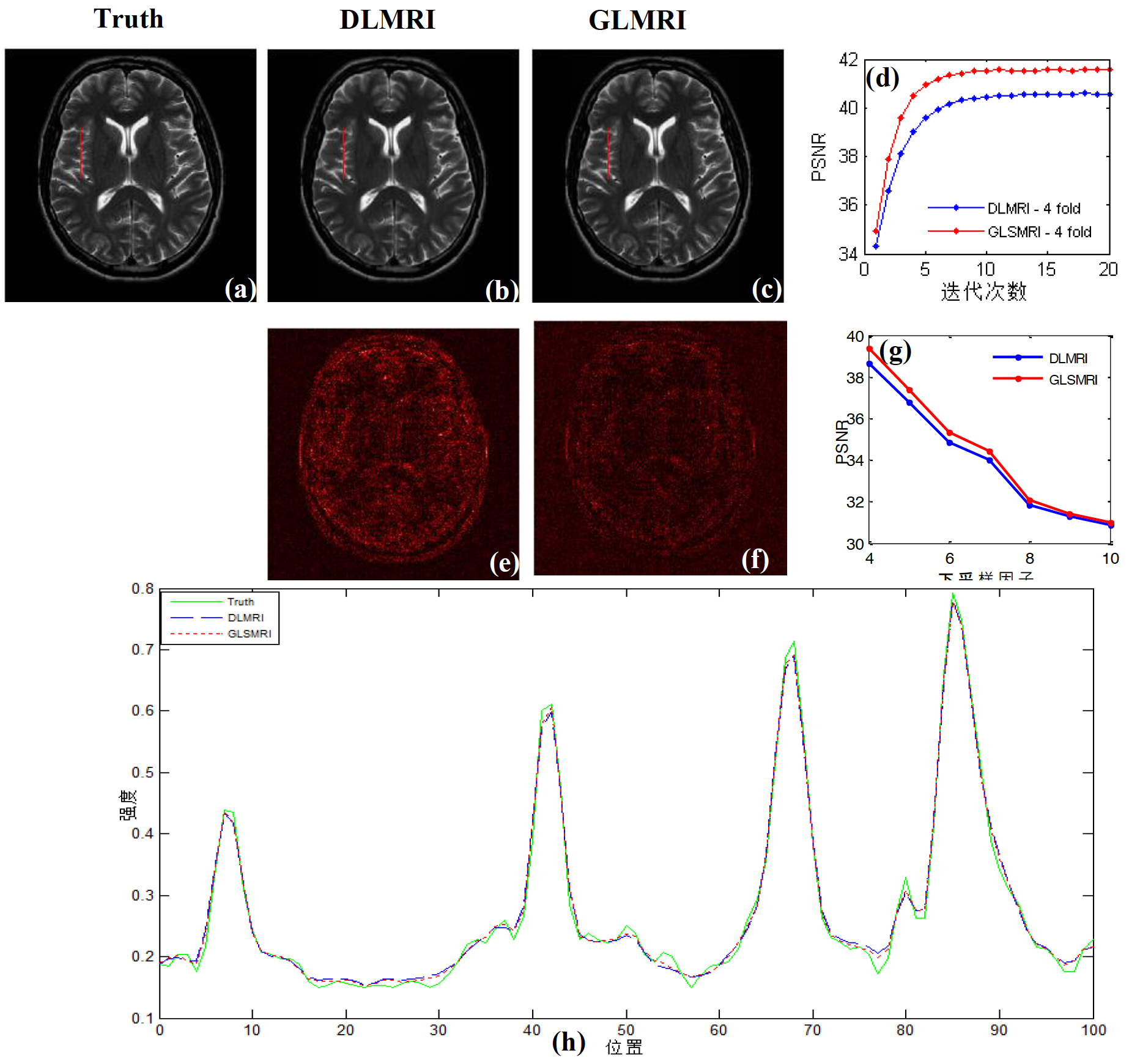
总结
本文主要介绍了MRI相关的一些领域知识以及CS在MRI上的一个应用, 后面会添加一些有关动态磁共振成像(dmri)的内容. 此外, 本文内容也是我的另一篇博文ADMM-net MRI和GAN-sr的主要背景知识.
待梳理
- dmri
Reference
- 1. Sparse MRI: The application of compressed sensing for rapid MR imaging
- 2. MR Image Reconstruction From Highly Undersampled k-Space Data by Dictionary Learning
转载请注明:Mengranlin » 点击阅读原文
