本文是在预研图像语义分割时所做的笔记, 主要对比分析了EFC-CRF(2011-Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials)和CRF-RNN(2015-Conditional Random Fields as Recurrent Neural Networks). 首先, 介绍传统方法EFC-CRF, 接着, 通过EFC-CRF的高效inference—mean-field-approximation引出其神经网络版CRF-RNN. 最后, 简单总结这两个方法.
目录
EFC-CRF
在图像语义分割里, 对于CRF的几种使用方式为: 单像素模型(unary potential)、图像快模型、近邻元素或近邻图像快模型(pairwise potential). 对于pairwise potential, 由于对像素 之间的关系进行建模, 理论上其最终效果梗接近图像本身的语义, 但这种模型有一个弊端: pairwise的规模越大, 在进行inference的时候越慢, 尤其是EFC-CRF这种全连接CRF模型. 全连接意味着要对所有像素对进行建模. 以256x256的图像为例, 就会有$\binom{256*256}{2} = 2147450880$个像素对, 这么大的模型, 在inference的时候会非常慢. 而EFC-CRF的主要贡献之一就是对inference的提速, 主要表现在两方面:
- mean-field approximation(mfa).
- 将mfa中的Message passing(pairwise potential)运算看成高维滤波问题, 进而用高效的permutohedral lattice进行求解.
接下来, 本文将介绍EFC-CRF的模型以及mean-field approximation. EFC-CRF的全连接模型为:
\[E(x) = \sum_{i}{\psi_{\mu}(x_i)} + \sum_{i < j}{\psi_{p}(x_i, x_j)} \tag{1}\]其中$i, j$是像素的索引, $\psi_{p}(x_i, x_j)$为pairwise potential, 也就是全连接的数学模型, 在EFC-CRF中是gaussian kernel的线性组合:
\[\psi_{p}(x_i, x_j) = \mu(x_i, x_j)\sum_{m=1}{K}w^{(m)}k^{(m)}(f_i, f_j) \tag{2}\]在实际应用中, 用了两个gaussian kernel:
\[\psi_{p}(x_i, x_j) = \mu(x_i, x_j)\{ w^{(1)} exp(-\frac{\left | p_i-p_j \right |^{2}}{2\theta_{\alpha}^2} - \frac{\left | I_i-I_j \right |^{2}}{2\theta_{\beta}^2}) + w^{(2)} exp(-\frac{\left | p_i-p_j \right |^{2}}{2\theta_{\gamma}^2}) \} \tag{3}\]两个kernel分别为: appearance kernel(ak)和smoothness kernel(sk). ak基于观察:相近的具有相似颜色的像素属于同类, 其中, $\theta_{\alpha}$控制了相近度, $\theta_{\beta}$控制了颜色的相似度. sk用于移除小的孤立区(注意, 这里的$\theta_{*}$从数据学习得到). 另外$\mu(x_i, x_j)$(Potts model, $\mu(x_i, x_j) = \left [ x_i\neq x_j \right ]$)被称作兼容项, 用于惩罚临近相似像素被打了不同的标签, 在EFC-CRF中, 对标签的建模并不是很精细, 而CRF-RNN对此有了更精细的建模.
模型到这基本介绍完了, 后面都是些通用的东西了, 即图像标签的Gibbs distribution:
\[P(x|I) = \frac{1}{Z}exp\left ( E(x) \right ) \tag{4}\]然后, 我们的inference就是极大化这个后验概率(MAP), 也就是解决如下问题:
\[x^{*} = arg max P(x|I) \tag{5}\]我们前文提到的全连接模型复杂性就体现在后验概率这, 这个优化问题中的$P(x|I)$有大规模的pairwise potential, 因此用常规的优化算法或者暴力穷举来解决这个问题回发现每一步的概率更新计算量都很大, 鉴于此, EFC-CRF的高效inference就采取了前文提到的两项优化工作, 总结起来就是: 在mean-field近似求解框架下对里面的pairwise potential用高效的滤波技术再提速.
本节的后半部分将着重介绍该近似inference算法: mean-field approximation, 此外为了加深理解, 我会对算法中的每一步用图辅以说明. 首先, 回顾下我们的问题: 计算后验概率$P(x|I)$比较低效. EFC-CRF的做法就是将这个复杂的后验分布简化为Q, 然后在最小散度$D(Q||P)$下对Q进行迭代更新, 在满足实际需要的精度要求后, 我们就得到了原始后验概率分布的近似解. 最终, 得到 的近似分布为:
\[Q_i(x_i=l) = \frac{1}{Z_i}exp \left \{ -\psi_{\mu}(x_i) - \sum_{l' \in L} \mu(l,l') \sum_{m=1}^{K} w^{(m)} \sum_{j \neq i} k^{(m)}(f_i,f_j)Q_j({l}') \right \} \tag{6}\]接着, 将该公式构造成迭代的形式, 就得到了最终的mean-field approximation求解框架:

从EFC-CRF到 CRF-RNN
我对于CRF-RNN的理解就是: 将mean-field approximation的一次迭代中的计算步骤定义成相应的layer, 如: 卷积层, 反卷积层. 由这些layer构成一个神经元或者说一个计算block, 然后, 将这些神经元recurrent后就形成了RNN神经网络. 为了对次描述有更深刻的认识, 下面我会用比较多的图来解释mean-field approximation的计算过程, 这个清楚了, 对CRF-RNN的网络细节也就清楚了.
像素关系
任意像素$i$为某标签$l$的概率由图像所有像素为$l$的概率共同决定, “共同决定”涉及到加权和, 加权的方式由pairwise potential中的kernel 个数$m$决定, 在EFC-CRF和CRF-RNN有两种加权方式: Appearance kernel, Smoothness Kernel, 个人觉得kernel就像是某种特定的视角. 像素之间的关系如图2(a-c)所示:
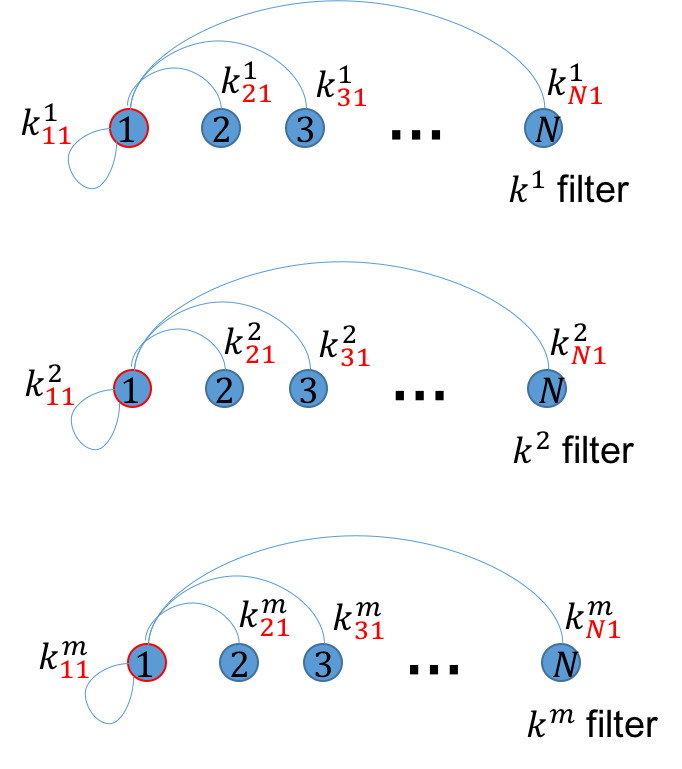
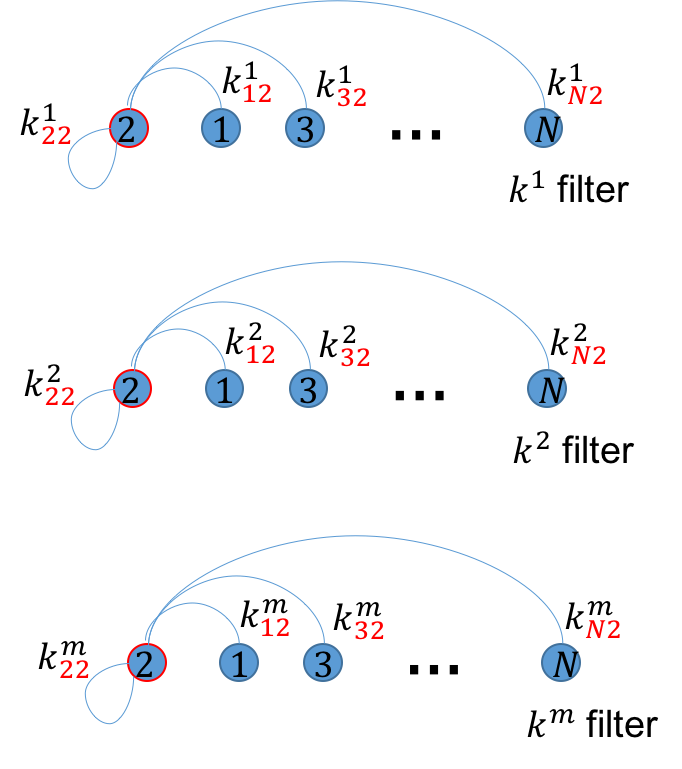
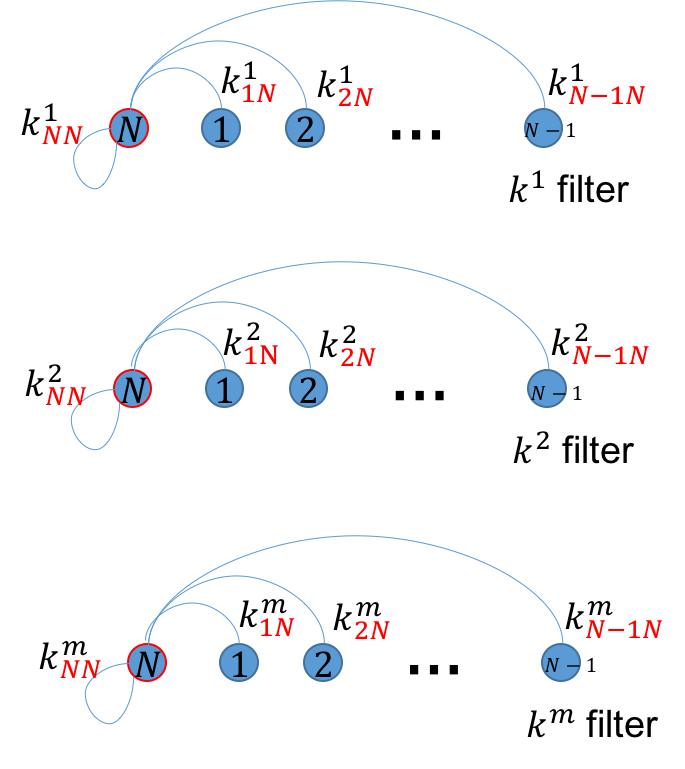
注意, $k_{ij}^{m}$中的下标代表$i, j$像素的关系, $m$代表具体的关系(视角), 如: 是Appearance kernel还是Smoothness kernel.
计算(Message Passing、Weighting Filter Outputs)
这里给出具体的像素标签概率Message Passing和Weighting Filter Outputs的计算流程, 如图3-5(a-c)所示:
注意: 像素之间的关系权重$k_{ij}^{m}$只于图像相关于标签没关系. 图看到这里我们需要知道图像中的像素是如何将标签$l$的概率传导给目标像素的.
计算(Compatibility Transform、Add unary Potentials、Normalization)
这部分计算内容相对容易, 也比较直观: 经过Message Passing和Weighting Filter后(结合了图像特征, 体现着后验), 再通过卷积(这里的卷积核体现标签的关系或者说兼容性)进一步更新目标像素各个标签的概率, 然后整合Unary potential, 最后进行归一化, 这样 就更新了概率分布.
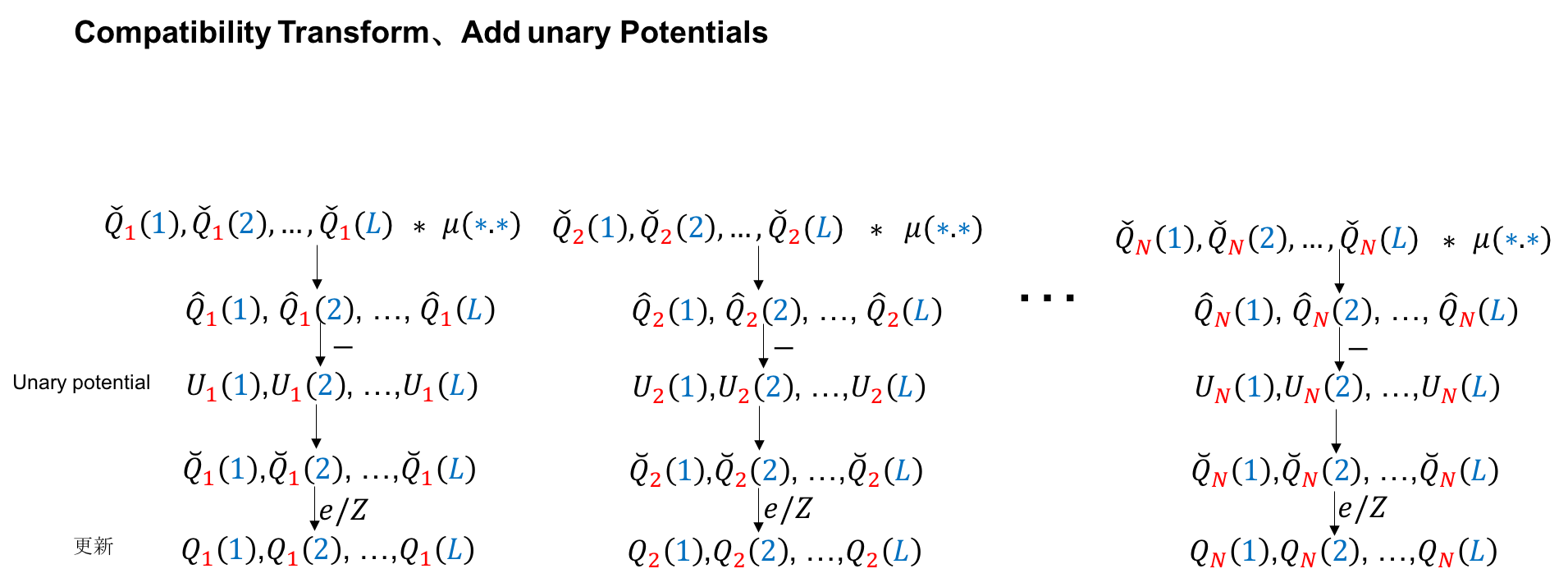
Mean-field approximation流程图
把上面提到的计算流程拼接起来, 看下整体的流程:
mean-field(一次迭代)与RNN神经元的对应
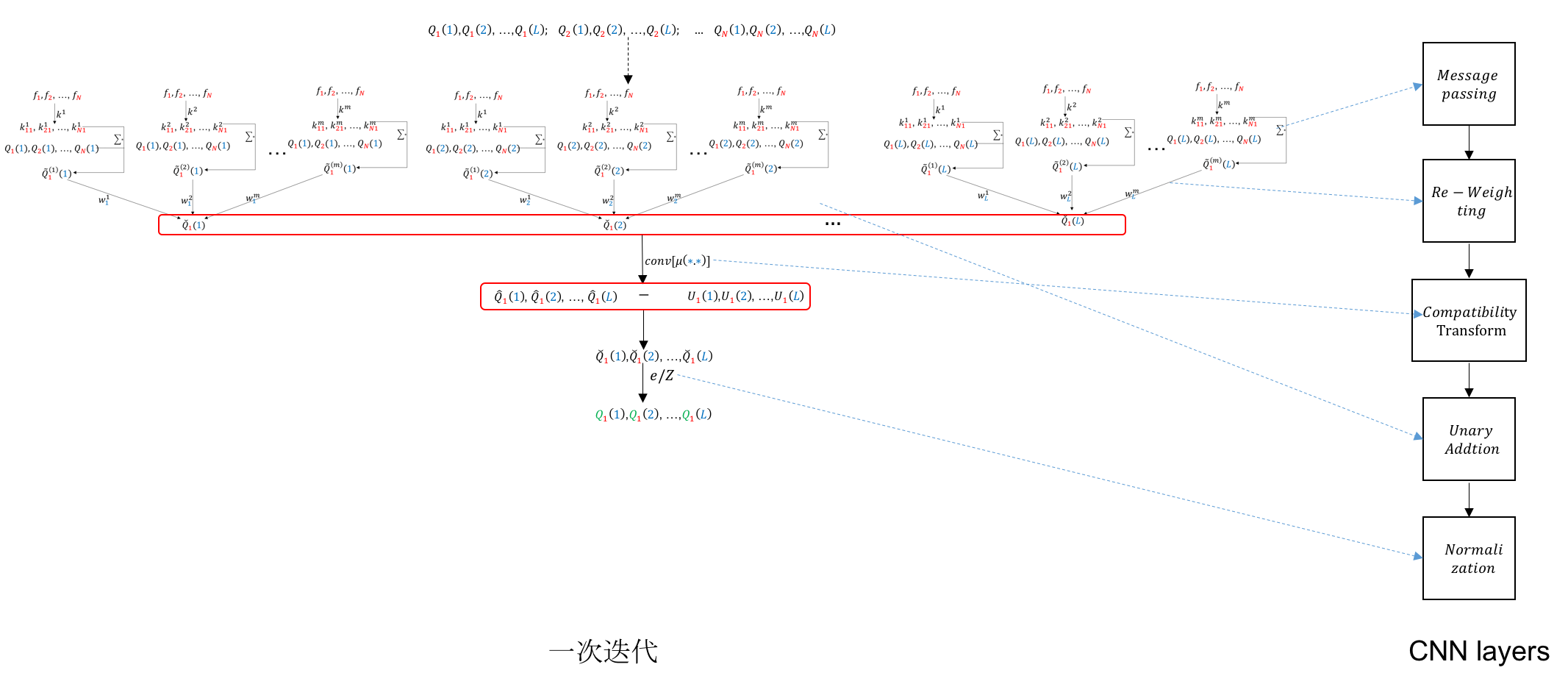
CRF-RNN网络
把图8中的CNN layers作为一个神经元进行recurrent后就构成了CRF-RNN这篇论文的网络结构:
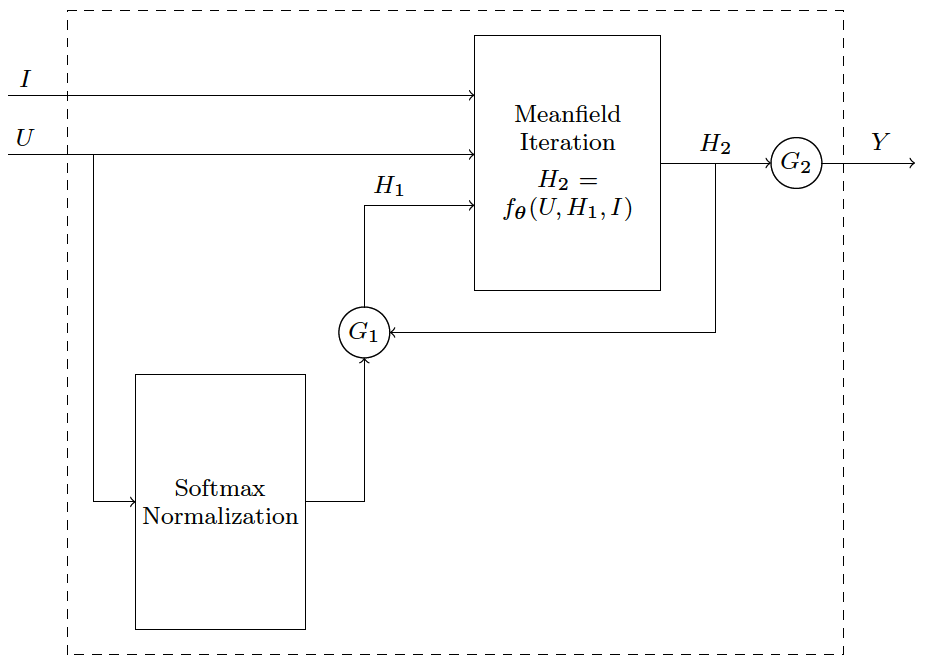
存疑点
我对EFC-CRF中的模型对于smoothness kernel有一点疑问, 原文提到这项约束可以去除孤立点, 仔细分析下, 我觉得目前的模型只是可能去除孤立点, 理由如下: 像素$i$的标签$l$概率由其他像素的$l$标签概率和权重共同决定, 而smooth kernel约束了图的权重, 从而模型上支持去除孤立区. 然而, 图权重对任意标签具有同等约束作用. 我想了下, 如果不优化原有模型, 就要看各个标签概率在同样约束下的最终竞争能力了. 举例说明: 要看图中黄色临域(smoothness kernel控制)内黑白标签在同等权重下的竞争能力, 如图所示:
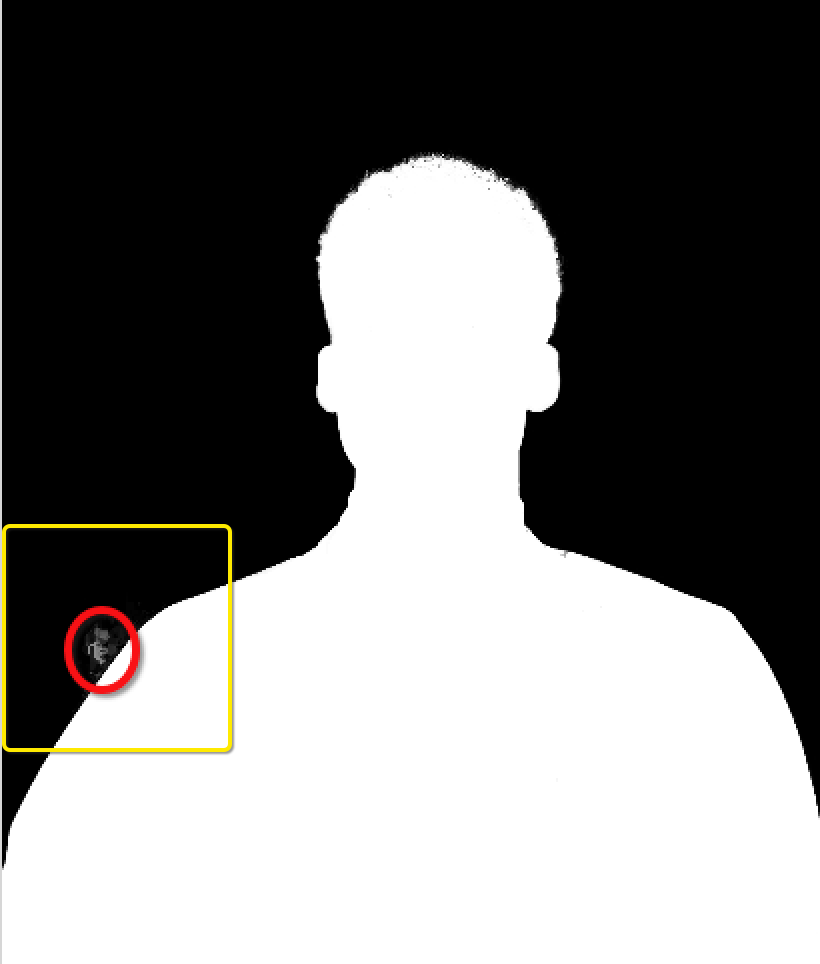
总结
图像语义分类的EFC-CRF传统方法和CRF-RNN总结完了, 个人认为这两个方法的数学模型一致,可以认为后者是神经网络版的crf, 只不过有些局部的改进, 如: 标签的关系模型不再用 Potts model, 对标签间的关系做了更细致的建模. 此外, 这里的 Unary Potential提供的分类结果很重要, 所以CRF-RNN中用了效果比较好的fcn-8s-pascal.caffemodel作为Unary potential, 我对Unary potential和CRF-RNN的理解是: 前者提供基础能力, 后者加强图像的语义结果. 另外, CRF-RNN对神经网络模型的建模方式同我之前写的一篇博文里介绍的ADMM-net-CS-MRI建模方式类似.
待梳理
- permutohedral lattice
Reference
- 1. Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials
- 2. Conditional Random Fields as Recurrent Neural Networks
转载请注明:Mengranlin » 点击阅读原文
