目录
- 梯度下降(Gradient Descent—GD)
- 共轭方向法(Conjugate Direction—CD)
- 共轭梯度法(Conjugate Gradient—CG)
- 变尺度法(Variable Metric Method—DFP)
- 总结
- Reference
本文是关于求解的, 也是自己对求解方面知识的一次总结. 文章主要介绍了无约束极值问题的一些常用方法, 同时也 是CNN这篇文章中Hessian Free Optimization的补充材料. 本文借助教材« 运筹学 »中 无约束极值问题的解法 完成了 这份补充材料. 此外, 我还希望这份材料可以作为教程来帮助更多的人解惑, 所以在行文上尽可能杜绝”显然”、 “易知”; 在证明 的时候尽可能给出这样做的思路, 所以文中有很多我自己的观点、方法, 当然也可能有不严谨的地方.
梯度下降(Gradient Descent—GD)
无约束极值问题可以被描述为:
\[min f(x), X \in E^n \tag{0}\]假设目标函数具有一阶连续偏导数, 并存在极小值点$ X^* $. 现在以$ X^k $作为对极小值点的第$ k $次近似, 那么第$ k+1 $次近似可被描述为 $ X^{k+1} = X^k + \lambda P^k$, 注意, 这里的步长$ \lambda $和方向向量$ P^k $都是不知道的. 我们这样建模的目的就是寻找一种求解方式使得$X^k$迭代下降, 而我们接下来阐述的GD算法就是能够达到此目的的一种方法, 进一步说就是对$ \lambda $和$ P^k $进行求解的一种方法. 接下来本文将介绍GD算法是如何对其进行具体求解的, 通过以下几个步骤展开我们的话题:
- 泰勒级数分析 —— 通过一阶泰勒级数展开来对方向向量进行理论分析, 也可以说是给出其可行域.
- GD的方向向量 —— 在该理论分析的基础上引出GD中所使用的方向向量$ P^{*}$, 即: GD是怎么求方向向量的.
- $\lambda$求解 —— 介绍几种求步长$ \lambda $的方法.
- 纸笔计算—— 如果有一天计算机没了, 我们可以用纸笔来做GD(多么牛批的解释).
- GD伪代码 —— 指导编码.
- 小结—— 获奖感言
1. 泰勒级数分析:
本节主要是站在理论制高点搔首弄姿的告诉你什么样的方向$P^k$是ok的, 什么样的方向是不ok的. 首先, 我交代下通过理论分析所得到的结论: 在$ X^k $ 的附近 充分小 的距离内, 只要$ P^k $与$ X^k $的梯度$ \nabla f(X^k) $的夹角大于$ 90^o $, 那么沿$P^k$行走就可以__改善__结果, 换句话说可以使目标函数进一步朝极小值迈进. 如果你对这个结论有了感性的认识, 那么可以不继续向下看了, 直接跳到下节吧. 接下来进行理论分析如何获得如上结论: 首先, 对原函数$ f(X) $进行一阶泰勒展开, 临域为$\lambda P^k$. 展开式为:
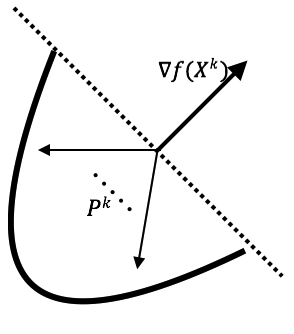
\[f(X^{k+1}) = f(X^k + \lambda P^k) = f(X^k) + \lambda \nabla f(X^k)^T P^k + o(\lambda) \tag{1}\]其中, 高阶项$ o(\lambda) $满足: $ \lim_{\lambda \rightarrow 0} \frac{o(\lambda)}{\lambda} = 0 $.(这个条件不满足是没办法用低阶项对原函数进行近似的, 你可以不严谨的想一个bad case: 不连续的函数). 也就是说, 在$ \lambda $充分小的时候, 我们可以忽略高阶分量的影响. 现在只考虑$ \lambda \nabla f(X^k)^T P^k $. 我们发现, 只要$ \nabla f(X^k)^T P^k < 0$就可以保证目标函数向极小值迈进, 即: $ f(X^k + \lambda P^k) < f(X^k) $, 至此, 理论分析结束. 我们要注意一点: 分析并没有给出具体的$ P^k $求解, 而是从微分的角度告诉我们 哪些 方向可以减小目标函数值. 我觉得很多时候我们不会记得住复杂的细节, 所以看完一段理论后最好能总结成一句话或者绘制一个图片, 哪怕是没那么严谨的. 这里我给出的助记总结是: “梯度方向的钝角区域可改善结果”, 同时绘制相应的助记图形, 如图1所示:
2. GD的方向向量:
前一节的泰勒级数分析没有给出具体的方向向量$ P^k $, 而是一种实操准则, 并不能用代码实现. 本节给出GD算法在该准则下的$P^k$具体求解, 同样, 先抛出结论: 沿$ P^k = -\nabla f(X^k) $ 方向行走可以使函数值下降最快, 负梯度方向也就意味着该钝角是$ {180}^o $, 接下来, 给出结论的推导过程: 我们在前文提到, 只要$ \nabla f(X^k)^T P^k < 0$就可以保证目标函数向极小值迈进, 由向量的内积我们可得到:
\[\nabla f(X^k)^T P^k = \left \| \nabla f(X^k) \right \| \cdot \left \| P^k \right \| {cos}^\theta \tag{2}\]式中,$ \theta $为向量$ \nabla f(X^k) $与$ P^k $的夹角. 当$ \theta = {180}^o, {cos}^\theta = -1$时$ \nabla f(X^k)^T P^k$最小. 此时$ \nabla f(X^k) $与$P^k$方向相反, 这样结论得证.
结合前两节我们得到这样的结论: 在$ X^k $ 附近 充分小 的距离内, 只要沿着$X^k $的梯度$ \nabla f(X^k) $反方向迈进, 可以使函数值下降最快, 这就是我们常听到的沿反向梯度反方向走下降最快的理论解释. 最后, 我们要确定步长$\lambda$.
3. $\lambda$求解:
这里只介绍最优一维搜索算法, 想法比较直观, 即: 使$ \lambda $满足:
\[\nabla f(X^k - \lambda \nabla f(X^k)) = 0 \tag{3.1}\]当然也有(零向量特点):
\[\nabla f^T(X^k-\lambda \nabla f(X^k)) \nabla f(X^k) = 0 \tag{3.2}\]这样求得的$\lambda$就是负梯度方向上的最佳步长. 此外, 如果$f(X)$具有二阶连续偏导数, 也可在$X^k$做$ f(X^k-\lambda \nabla f(X^k)) $的泰勒展开, 然后用低阶项进行近似:
\[f(X^k - \lambda \nabla f(X^k)) \approx f(X^k) - \nabla f^T(X^k)\lambda \nabla f(X^k) + \frac{1}{2}\lambda \nabla f^T(X^k) H(X^k)\lambda \nabla f(X^k) = 0 \tag{3.3}\]得到:
\[{\lambda}^k = \frac{\nabla f^T(X^k \nabla f(X^k)}{\nabla f^T(X^k H(X^k)\nabla f(X^k} \tag{3.4}\]接着, 负梯度方向取单位向量$ P^k = -\frac{\nabla f(X^k)}{\left | \nabla f(X^k) \right |}$, 求${\lambda}^k$:
由
\[\nabla f(X^k + \lambda P^k) \approx f(X^k) + \lambda \nabla f^T(X^k) P^k + \frac{1}{2} \lambda {P^k}^k H(X^k) \lambda P^k = 0 \tag{3.5}\]求得:
\[{\lambda}^k = -\frac{ \nabla f^T(X^k)P^k} { {P^k}^T H(X^k) P^k } \tag{3.6}\]将$ P^k = -\frac{\nabla f(X^k)} {\left | \nabla f(X^k) \right |}$带入 3.6 式:
\[{\lambda}^k = \frac{\nabla f^T(X^k) \nabla f(X^k) \left \| \nabla f(X^k) \right \|} {\nabla f^T(X^k) H(X^k) \nabla f(X^k)} \tag{3.7}\]4. 纸笔计算:

5. GD伪代码:

6. 总结:
GD算法是比较简单的方法了, 在实际应用中其实没必要关注这么多理论细节. 这个方法有个缺陷: 泰勒级数分析也就意味着这是个临域方法, 从而对于复杂函数(多个极值点)可能求出的解是局部最小值. 因为每次迭代都是选择临域最优解, 所以GD法是个贪心算法. 如果模型比较简单比如单峰函数, 用这个方法就可以了, 对于复杂的模型, 这个求解方法能力是不够的. 另外再提醒一下: 负方向最速下降的理论基础是泰勒级数展开, 因此必须在临域内, 他才是使目标函数下降最快的. 另外GD方法还有个特点: 当目标函数的等值线偏扁平的时候, 收敛速度就没那么快了, 因此在实际应用中通常结合GD和其他收敛速度快的方法一起使用.
共轭方向法(Conjugate-Direction—CD)
这一部分讨论稍微高阶点的方法: 共轭方向法. 所谓共轭就是正交概念的推广: 非0向量$X$与$Y$关于对称正定矩阵$A$共轭, 有$X^TAY=0$. 由此可见正交的两个向量是$I$共轭的. 该部分的讨论围绕正定二次函数极小值问题. 正定二次函数的极小值问题为:
\[min f(X) = \frac{ 1 }{ 2 }X^TAX + B^TX + c \tag{ 0 }\]其中, $A$是对阵正定矩阵, $B \in E^n, X \in E^n$. 对于这个问题, 有如下定理: 如果向量组$P^{ i }, i = 0, 1, 2, …, n-1$是$A$共轭的, 那么从任意$X^0$出发只要不重不落的沿着向量组里的向量方向迭代更新就可以收敛到极小值点$X^*$. 对于这个定理我给出自己稍好理解的解释:
由于$P^{ i }$是$A$共轭的, 那么$P^{ i }$一定是线性独立的, 又因为向量组有$n$个向量, 所以综合这两点我们得到:$X^0, X^*$一定在$P^{ i }$张成的线性空间里(因为该向量组是基), 因此有:
\[\begin{cases} \alpha_0P^{0} + \alpha_1P^{1} +, ..., + \alpha_{n-1}P^{n-1} = X^0 \text{ ,(a)}\\ \alpha_0'P^{0} + \alpha_1'P^{1} +, ..., + \alpha_{n-1}'P^{n-1} = X^* \text{ ,(b)} \tag{1} \end{cases}\]$(b) -(a)$并整理得:
\[X^0 + (\alpha_0' - \alpha_0)P^{0} + (\alpha_1' - \alpha_1)P^{1} +, ..., + (\alpha_{n-1}' - \alpha_{n-1} )P^{n-1} = X^* \tag{ 2 }\]显然左式可写成如下迭代格式:
\[X^{ i-1 } + (\alpha_{i-1}' - \alpha_{i-1} )P^{i-1} = X^{ i } \tag{ 3 }\]其中, $i \in { \begin{Bmatrix} 1, 2, 3,…,n \end{Bmatrix} }$, 显然经过n次迭代即可收敛到$X^{ * }$, 结论得证. 我认为: 单纯为了证明这个定理只需要知道向量组是向量空间的基即可, 并不需要满足$A$共轭. 然而, 我这个证明相比较教材中的证明是有缺陷的, 即: 没办法给出迭代中${\lambda}^k$的具体 解法, 而教材的证明既给出了证明, 又给出了${\lambda}^k$的一种解法—最优一维搜索, 而该解法在”$P^{i}$是$A$共轭的”条件下使得$ \nabla f(X^n)$为0,进而得到了极小值点. 因此教材中的证明既给出了理论验证又给出了求解方案.(对于这个细节我会单独在另外一篇博客里给出更详细的解释) 说到了这, 共轭方向法也算是呼之欲出了, 即: 如果给定任意已知的$A$的共轭向量组$ { \begin{Bmatrix} P^{(0)}, P^{(1)}, …, P^{(n-1)} \end{Bmatrix} } $, 那么只要按照如下方式迭代就可以求得正定二次函数的极小值:
\[\begin{cases} \lambda_{k}: \min_{\lambda} f(X^{(k)} + \lambda P^{(k)}) \text{ , 最优一维搜索(前面已铺垫) }\\ X^{(k+1)} = X^{(k)} + \lambda_{k} P^{k}, k = 0, 1, 2, ... ,n-1 \\ \tag{4} \end{cases}\]这就是共轭方向法的内容了, 记住两个关键点即可: 1). 共轭基 2). 用最优一维搜索求${\lambda}_*$. 当然, 到这里就有了新问题了: 这里只是点明了对基的要求, 而没有明确给出基的求解方法, 那么具体怎么获得满足要求的基呢? 接下来讨论的共轭梯度法就是一种具体的求解方法.
共轭梯度法(Conjugate-Gradient—CG)
由前面的描述我们知道共轭梯度法(CG)和共轭方向法(CD)的关系: CG是在CD框架下的一种具体解法, 直白点的描述就是: 前者能写代码, 后者只能看看(我皮吗?). 接下来给出CG的推导过程. 首先, 回顾下正定二次函数问题的极小值特点: 1. 唯一存在; 2. 其理论解为: $= -A^{-1}B$.(看到这是否有种脱裤子放屁的感觉:”既然都知道解了, 为毛还搞些有的没的”. 其实有一丢丢基础的人都清楚: $A^{-1}$是很难求的, 因此也就有人会想到利用稀疏化技术对其简化, 比如我以前做的CS问题就涉及这方面的内容. 不过, 即使知道, 我初学的时候还偶尔会脑抽犯嘀咕.), 因此, 对于这个任务只要按照方向梯度法执行固定的步数(找到极值点)就可以了. 那么CG是如何工作的呢? CG是怎么满足CD的呢? 仍然先把结论抛出来: 在一组正交基中寻找满足$A$共轭的基, 满足特定条件的基找完了算法也就结束了(伴随着${\lambda}_*$的求解), 我对比观察后发现: 这里基的找法同拉格姆-施密特正交化法类似. 最后, 我用一句话总结CG的核心思想: 正交基中找共轭基. 这里补充个细节: 我们提到的正交基是由每次迭代的近似解$X^k$($k \in \begin{Bmatrix} 1, 2,…, n-1\end{Bmatrix}$)的梯度$\nabla f(X^k)$构成.(我仍然觉得, 如果你的工作重心在建模, 有如上的认识就够了, 因为不太可能自己去写CG. 另外, 这些内容是可以推导出CG的具体求解细节的, 前提是要有点耐心.) 下面进行推导:
首先, 我们回顾下确定$\lambda$的最优一纬搜索的内容:
\[\frac{df(X^{ k+1 })}{d\lambda} = \frac{df(X^{ k }+\lambda P^{ k })}{d\lambda } = \nabla f(X^{ k+1 }) P^{ k } = 0 \tag{ 5 }\]写近点, 后边方便看. 任取初始近似点$X^{0}$, 初始方向$P^{0} = - \nabla f(X^{0})$. 利用$(5)$的最优一维搜索我们可以依次确定$\lambda^{0}, X^{1}, \nabla f(X^{1})$. 此外, (5)也蕴含着(将$\nabla f(X^{1})$带入$5$式): $\nabla f(X^{1}) \nabla f(X^{0}) = 0$. duang, 我们前文描述的正交基向量出来了, 接着就是从中找共轭基向量了. 再次先交代如何找共轭基向量, 即: 共轭条件下的待定系数. 交代完找的方法后小结一下以加深印象: $k$次迭代中做的事情就是: 确定第$k$个正交基向量, 从中找第$k$个共轭基向量. 我把第$k$次迭代具体做的事推导出来, 那么整个求解流程也就讲完了.
进入第$k$次迭代时, 我们有如下已知项:
\[\begin{cases} X^{k-1}, \text{k-1次迭代的极小值估计} \\ \nabla f(X^{0}), \nabla f(X^{1}), ..., \nabla f(X^{k-1}), \text{正交向量组} \\ P(X^{0}), P(X^{1}), ..., P(X^{k-1}), \text{共轭向量组} \end{cases}\]再次重写下递推关系式:
\[X^{k} = X^{k-1} + \lambda^{k-1} P^{k-1}\]首先, 通过最优一纬搜索依次确定$\lambda^{k-1}, X^{k}, \nabla f(X^{k})$, 这样就得到了新的正交基向量$\nabla f(X^{k})$,(你可能很好奇为什么这么求就保证了$\nabla f(X^{k})$就是正交基向量,完成推导后会给出解释.) 然后, 用新的正交向量组表示共轭基向量$P^{k}$, 同时又要满足共轭条件, 即:
\[\begin{cases} P(X^{k}) = -\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0}) \\ P(X^{k})^TAP(X^{k-1}) = 0 \\ P(X^{k})^TAP(X^{k-2}) = 0 \\ ... \\ P(X^{k})^TAP(X^{0}) = 0 \end{cases} \tag{ 6 }\]我们的目的是把方程组中的${\begin{Bmatrix}\alpha_{k-1}, \alpha_{k-2},…, \alpha_{0}\end{Bmatrix}}$求出来, 解决该问题的一个思路就是 表示一致, 具体做法就是将所有的共轭等式的左侧用梯度表示, 因此, 尝试找$AP(X^{i}), i \in {\begin{Bmatrix} 1, 2, 3 \end{Bmatrix} }$ 的梯度表达, 这里由梯度函数与极小值递推公式可获得我们想要的东西, 由:
\[\begin{cases} \nabla f(X^{k}) = AX^{k} + B \\ \nabla f(X^{k-1}) = AX^{k-1} + B \\ X^{k} = X^{k-1} + \lambda^{k-1} P^{k-1} \end{cases}\]得:
\[\nabla f(X^{k}) - \nabla f(X^{k-1}) = A(X^{k} - X^{k-1}) = \lambda_{k-1}AP^{k-1} \tag{ 7 }\]用同样的方法可以将所有的$AP(X^{i})$找到. 这样将$(6)$中的所有共轭条件等式进行梯度表达, 首先:
\[\begin{cases} \\ (-\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0}))^TAP^{k-1} = 0 \\ (-\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0}))^TAP^{k-2} = 0 \\ ... \\ (-\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0}))^TAP^{0} = 0 \end{cases} \tag{ 8 }\]接着将形如$(7)$的式子对$(8)$中的所有$AP(X^{i})$进行替换便得到了我们前文所期望的梯度表达式:
\[\begin{cases} \\ [-\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0})]^T[\nabla f(X^{k}) - \nabla f(X^{k-1})] = 0 \\ [-\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0})]^T[\nabla f(X^{k-1}) - \nabla f(X^{k-2})] = 0 \\ ... \\ [-\nabla f(X^{k}) + \alpha_{k-1} \nabla f(X^{k-1}) +, ..., \alpha_{0} \nabla f(X^{0})]^T[\nabla f(X^{1}) - \nabla f(X^{0})] = 0 \end{cases} \tag{ 9 }\]利用正交, 整理简化得:
\[\begin{cases} \alpha_{k-1} \nabla f(X^{k-1})^T \nabla f(X^{k-1}) = -\nabla f(X^{k})^T \nabla f(X^{k}) \\ \alpha_{k-2} \nabla f(X^{k-2})^T \nabla f(X^{k-2}) = \alpha_{k-1} \nabla f(X^{k-1})^T \nabla f(X^{k-1}) \\ ... \\ \alpha_{0} \nabla f(X^{0})^T \nabla f(X^{0}) = \alpha_{1} \nabla f(X^{1})^T \nabla f(X^{1}) \end{cases} \tag{ 10 }\]玩一波多米诺骨牌, 得:
\[\begin{cases} \alpha_{k-1} = - \frac{\nabla f(X^{k})^T \nabla f(X^{k})}{\nabla f(X^{k-1})^T \nabla f(X^{k-1})} \\ \alpha_{k-2} = - \frac{\nabla f(X^{k})^T \nabla f(X^{k})}{\nabla f(X^{k-2})^T \nabla f(X^{k-2})} \\ ... \\ \alpha_{0} = - \frac{\nabla f(X^{k})^T \nabla f(X^{k})}{\nabla f(X^{0})^T \nabla f(X^{0})} \\ \end{cases} \tag{11}\]因此共轭方向为:
\[P(X^k) = -\nabla f(X^k) + \sum_{i=0}^{k-1} -\frac{\nabla f(X^{k})^T \nabla f(X^{k}))}{\nabla f(X^{i})^T \nabla f(X^{i})} \nabla f(X^{i}) \tag{ 12 }\]接下来尝试将将$12$写成递归的形式, 那么自然想到折腾$\sum$了:
\[\begin{matrix} P(X^k) = -\nabla f(X^k) + \\ -\frac{\nabla f(X^{k})^T \nabla f(X^{k})}{\nabla f(X^{k-1})^T \nabla f(X^{k-1})} \nabla f(X^{k-1}) + \sum_{i=0}^{k-2} -\frac{\nabla f(X^{k})^T \nabla f(X^{k}))}{\nabla f(X^{i})^T \nabla f(X^{i})} \nabla f(X^{i}) \tag{ 13 } \end{matrix}\]整理一下:
\[\begin{matrix} P(X^k) = -\nabla f(X^k) + \\ \frac{\nabla f(X^{k})^T \nabla f(X^{k})}{\nabla f(X^{k-1})^T \nabla f(X^{k-1})} \{-\nabla f(X^{k-1}) + \sum_{i=0}^{k-2} -\frac{\nabla f(X^{k-1})^T \nabla f(X^{k-1}))}{\nabla f(X^{i})^T \nabla f(X^{i})} \nabla f(X^{i}) \} \end{matrix}\]比较$(12)$和$(13)$很容易发现递归式:
\[\begin{cases} P(X^k) = -\nabla f(X^k) + \beta_{k-1} P(X^{k-1}) \\ \beta_{k-1} = \frac{\nabla f(X^{k})^T \nabla f(X^{k})} {\nabla f(X^{k-1})^T \nabla f(X^{k-1})} \end{cases} \tag{14}\]这样便完成了一次迭代, 总结一下一次迭代中所做的事情(k次迭代为例):
\[\begin{cases} 1. 最优一维搜索, 确定系数\lambda^{k-1} \\ 2. 更新极小值的近似解X^k \\ 3. 扩充正交基向量组, 即: 求正交基向量\nabla f(X^k) \\ 4. 扩充共轭基向量组, 即: 求共轭基向量P^k \end{cases}\]从迭代公式我能看出: 共轭梯度法每一步的决策方向由前面所有迭代中的梯度共同决定的, 而GD是只由当前的梯度决定, 所以CG方法是长时系统, GD是短时系统. 从程序设计的角度来看迭代中的内容, 容易总结出两件事:
- 步骤1、2使算法向前推进
- 步骤3、4起到了循环不变的作用[算法导论里有关于这个概念的介绍, 简单点说就是保持每次进入循环时目标变量($X^*$)的环境是不变的].
回顾整个算法, 迭代一直执行到共轭基向量组从空集${\Phi}$变成共轭基$\begin{Bmatrix} P^{0}, P^{1},…, P^{n-1}\end{Bmatrix}$. 到这里我把共轭梯度法讲完了, 建议老老实实推一遍公式, 像我一样nice的总结几个关键点, 以后再也别看这玩意了, 港真, 做模型的几乎不可能去优化这种底层计算. 然后就是加深印象的环节了, 老规矩: 手算、总结.
1. 纸笔计算:

2. 总结:
对于二次函数, 虽说伴随着找到共轭基(n次迭代)就找到了极小值点, 但是在实际应中由于数值计算的问题可能就不得行了. 对于这种情况千万不要增加迭代步骤了, 没什么意义, 毕竟共轭基都找到了, 可以试着以本次算法的估计$X^{n}$作为初始值再跑一遍代码. 冷静, 这里说的好生热闹, 可还是针对正定二次函数进行CG求解, 那么如何将其应用到非二次函数呢, 如果这个问题解决不了, 耶稣都不会让这个方法发表.
3. 非二次函数的共轭梯度法:
先简单谈谈我对推广方法的理解吧: 没有正定二次函数不要紧, 创造条件也要有, 怎么创造条件呢—-泰勒级数展开(啧啧, 还真是哪都有这个老小子). 这部分内容跟正定二次函数的求解基本一致, 因此简单说下流程, 然后指出在推广中所用到的一些近似关系.
假设我们的目标函数$f(X)$是严格凸函数并且具有二阶连续偏导数, 并且存在唯一极小值点. 跟前文保持一致性, 这里仍然分析进入第$k$次迭代所做的事情. 此时, 我们的已知项是:
\[\begin{cases} X^{k-1}, \text{k-1次迭代的极小值估计} \\ \nabla f(X^{0}), \nabla f(X^{1}), ..., \nabla f(X^{k-1}), \text{近似正交的向量组} \\ P(X^{0}), P(X^{1}), ..., P(X^{k-1}), \text{近似共轭的向量组} \end{cases}\]后面的步骤同前面是一样的, 我只提及个有区别的地方:
- $\nabla f(X^k)$ 跟前面正定二次函数中所求的梯度是不同的, 这里的梯度只是一个近似, 因为其根源在于: 我们是在泰勒级数展开这个近似函数的基础之上求出来的
- 这里的共轭是:$p^k$与$p^0, p^1,…, p^{k-1}$是关于$H(X^{k-1})$共轭的.
对于第二条, 形象点说: 由于$H(X^*)$是随着迭代而 变化 的, 所以这里的共轭是一种前向共轭. 共轭梯度法已整理完, 接下来介绍一种拟牛顿方法.
变尺度法(Variable Metric Method—DFP)
该方法的两个主要特点是:
\[\begin{cases} 1. 不用计算Hessian-Matrix \\ 2. 比梯度法收敛速度快, 尤其是对高维问题 \end{cases}\]1. 基本原理:
从极小值的更新模型$X^{k+1} = X^k + \lambda^k P^k$来看, 相比于最简单的梯度下降, 变尺度法对更新方向进行了 约束,(也可以将梯度下降理解成是有约束的, 即: 约束矩阵为恒等矩阵.) 其约束矩阵是二阶导数, 也就是他喵的Hessian-Matrix. 但在实际问题中, 由于模型的复杂性, 这个矩阵比较难求或者不能求. 变尺度法的做法就是对其进行近似估计, 接下来本文会依次 讲解: a). 变尺度法的极小值更新模型(带约束的梯度下降), b). 更新模型中约束矩阵的近似计算.
a. 变尺度法的极小值更新模型
假定我们的目标函数$f(X)$具有二阶连续偏导数, 并且其一阶倒数$\nabla f(X)$可求. 根据泰勒级数展开, 在$X^k$ 的附近($\Delta X$)有:
\[f(X) = f(X^k + \Delta X) \approx f(X^k) + \nabla f^T(X^k)\Delta X + \frac{1}{2} \Delta X^T H(X^k) \Delta X \tag{1}\]原函数的梯度近似为:
\[\nabla f(X) = \frac{\partial f(X^k + \Delta X)}{\partial \Delta X} \approx \nabla f(X^k) + H(X^k) \Delta X \tag{2}\]也就是:
\[\nabla f(X) \approx \nabla f(X^k) + H(X^k) \Delta X \tag{3}\]用$\nabla f(X^k) + H(X^k) \Delta X = 0$近似代替$\nabla f(X) = 0$可得到原函数极小值点的__近似__:
\[\begin{cases} \Delta X = -H^{-1}(X^k) \nabla f(X^k) \text{,=>} \\ X = X^k -H^{-1}(X^k) \nabla f(X^k) \tag{4} \end{cases}\]$X = X^k -H^{-1}(X^k) \nabla f(X^k)$就是变尺度法的极小值更新模型, $-H^{-1}(X^k) \nabla f(X^k)$也称作牛顿方向.
b. 更新模型中约束矩阵的近似计算
对于上面提到的牛顿方向, 如果原函数的二阶导数的Hessian-Matrix的逆$H^{-1}(.)$好求, 那么这个方法是目前为止介绍的 方法中收敛速度最快的. 然而, 由于现实因素的限制, 我们很多时候只能近似求$H^{-1}(.)$的逆. 接下来的部分就要根据 $H^{-1}(.)$的特点以及迭代求解这种方式所带来的逐步逼近的便利来对$H^{-1}(.)$进行:按照一定的准则, 逐步逼近. 我们希望: 每次迭代目标函数都有所下降, 近似逼近矩阵最终收敛于极小值点处的$H^{-1}(.)$的逆. 为了实现 这一目标, 后面的内容将这样介绍: 首先, 构建$H^{-1}(.)$的更新模型, 然后, 利用待定系数求出迭代模型中的未知部分.
最简单的 一种 更新模型是:
\[H^{-1}(X^{k+1}) = H^{-1}(X^{k}) + \Delta^k \tag{5}\]其中, $\Delta^k$是不知道的, $H^{-1}(X^{k-1})$是已知的, 那么问题就变成了求解$\Delta^k$(校正矩阵). 为了避免在推导的过程中产生混乱, 先把$k$次迭代(由于流程类似, 因此可类比回忆”一次迭代中所做的事情”)中的已知项、未知项以及求解 $H^{-1}(X^k)$在整个迭代求解中的作用理出来, 这些东西清楚了再利用待定系数配合一些假设来把$\Delta^k$推导出来.
假定 这会儿我们已经知道$H^{-1}(.)$是怎样进行更新的了, 在进入第$k$次迭代时, 我们首先会利用$H^k$(前一次迭代所做的更新) 、$\nabla f(X^k)$把牛顿方向$-H^{-1}(X^k) \nabla f(X^k)$求出来, 然后更新极小值$X^{k+1}$, 到这一步我们完成了一次迭代中的 向前推进算法 . 接着就要利用$X^{k+1}$、$H^{-1}(X^k)$依次把$\nabla f(X^(k+1))$、$H^{k+1}$求出来以完成一次迭代 中的 循环不变. 到这, 我把其中可能引起混乱的条目理清了, 开阔之, 我们求解$H^{-1}(k+1)$的目的是:
\[\begin{cases} 1. 求解H^{-1}(k+1)是为了:本次迭代的循环不变、下次迭代的极小值更新 \\ 2. 已知项: H^{-1}(X^k)、 \nabla f(X^k)、 X^{k+1}、 \nabla f(X^{k+1}) \\ 3. 未知项: \Delta ^k \\ 4. 求解目标: H^{-1}(X^{k+1}) \end{cases} \tag{6}\]接下来, 就要利用这些条件来进行待定系数求解了, 思路为: 在已知的信息中构造关于$H^{k+1}$的等式, 然后, 用$H^{-1}(X^k)+\Delta^k$对其进行替换, 这样就为求解$\Delta X^k$也就是$H^{-1}(X^{k+1})$提供了可能性. 由公式$(3)$, 我们可以得到如下近似关系:
\[\nabla f(X^{k+1}) \approx \nabla f(X^k) + H(X^{k+1})(X^{k+1}-X^{k})\]整理之:
\[\begin{cases} \Delta X^k \approx H^{-1}(X^{k+1}) \Delta G^k \\ \Delta X^k = X^{k+1} - X^{k} \\ \Delta G^k = \nabla f(X^{k+1}) - \nabla f(X^k) \end{cases} \tag{7}\]结合$(6)$, 我们知道$\Delta X^k$和$\Delta G^k$是已知项. 等式$(7)$构造好后, 用$H^{-1}(X^k) + \Delta^k$对$H^{-1}(X^{k+1})$ 进行替换, 得:
\[\Delta X^k \approx (H^{-1}(X^k) + \Delta^k) \Delta G^k \tag{8}\]整理得:
\[\Delta^k \Delta G^k \approx \Delta X^k - H^{-1}(\Delta X^k) (W^k)^T \tag{9}\]我们希望把$\Delta G^k$消掉, 这样$\Delta X^k$便求出来了, 直接试图通过矩阵运算的方式有点儿难以推进. 不妨方向思考: 给$\Delta^k$设计一个可以进行待定系数求解的形式, 即:
\[\Delta^k = \Delta X^k (Q^k)^T - H^{-1}(X^k) \Delta G^k (W^k)^T \tag{10}\]把$(10)$带入$(9)$之后, 比对左右两项可以得到:
\[\begin{cases} (Q^k)^T \Delta G^k = 1 \\ (W^k)^T \Delta G^k = 1 \tag{11} \end{cases}\]问题转化成求解$Q^k、W^k$, 仍然思考给这两个向量设计一个简单的形式. 看$(10)$, 如果$H^{-1}(.)$是对称正定的, 显然$Delta^k$ 也是对称正定的. 在这个假设条件下, 对$(10)$的右侧做进一步的简化, 使其具有$scalar by vector$的形式, 其中只有$scalar$ 是未知的. 因此有:
\[\begin{cases} Q^k = \eta^k \Delta X^k \\ W^k = \xi^k H(X^k)\Delta G^k \end{cases} \tag{12}\]将$(12)$带入$(11)$可得待定系数:
\[\begin{cases} \eta^k = \frac{1}{(\Delta X^k)^T \Delta G^k} \\ \xi^k = \frac{1}{(\Delta G^k)^T H^T(X^k) \Delta G^k} \end{cases} \tag{13}\]待定系数求得后, 校正矩阵就可求了, 这里直接写结果了:
\[\Delta^k = \frac{\Delta X^k (\Delta X^k)^T}{(\Delta X^k)^T \Delta G^k} - \frac{H^{-1}(X^k)\Delta G^k (\Delta G^k)^T H^T(X^k)}{(\Delta G^k)^T H^T(X^k)\Delta G^k} \tag{14}\]校正矩阵的求解确定后, 我们就可以对更新模型中的约束矩阵进行近似计算了. 值得注意的是, 变尺度法的近似求解不止这一种. 时刻牢记: 要把模型与模型求解区分开, 你可以提出不同于$(5)$的更新模型, 你可以给出不同的求解方案, 当然你也可以有不同 的求解假设. 这就意味着: 只要满足(a)中的更新模型, 后面的具体求解你是可以提出不同方案的.
总结
对比本文介绍的梯度下降法(GD)、共轭梯度法(CG)、步长加速法(DFP), 会发现他们的大体流程基本一致, 主要的区别在于极小值 更新模型中的方向向量, GD选择了负梯度作为方向向量、CG在由梯度张成的空间内选取共轭梯度作为方向向量、DFP利用Hessian-Matrix 对梯度方向进行校正后作为方向向量. 可见他们都跟梯度这个梗有关, 要么直接用、要么在线性空间内选取、要么校正一下. 第一稿就总结到这里了, 我觉得这种基础性的东西如果写的不仔细点还不如不写, 因为本身就没多少东西; 另外, 本人对博客是这样理解的: 博客不同于论文, 前者应该承担 更多的教程角色, 因此, 博客里应该尽可能的少出现”显然…“这样的字样, 同时, 应该给出证明的思路, 所以一定会比论文啰嗦. 最后谈一点个人 的感受: 看理论的话, 最好自己去证明一下, 意淫下作者的思路, 只有这样, 印象才深刻.
Reference
转载请注明:Mengranlin » 点击阅读原文
